Inverse Kinematics

Inverse Kinematics#

The inverse kinematics (IK) is to determine joint variables given end-effector position and orientation. IK is important in robotics because it allows to transform motion specification of operational space into that of joint space. But IK is complex, because

FK is nonlinear, and thus IK is not always possible to find closed-form solutions.
Multiple IK solutions may exist, e.g., for a redundant robot arm.
There might be no feasbile IK solutions, e.g., due to mechanical limits.

In this lecture, we only talk about IK that has a closed-form solution. This is only the case for some special-structured robot arms. For more generalized case, we will leave IK in future lectures.

IK of Three-link Planar Arm#

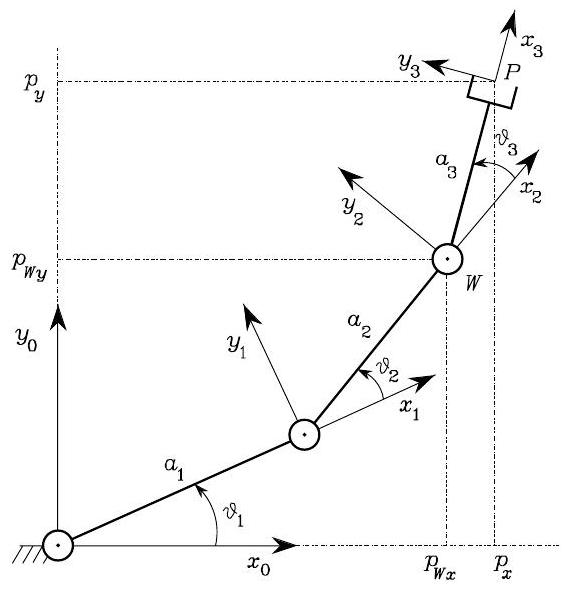
../_images/3link_arm1.jpg — Fig. 35 A three link robot arm#

Suppose the pose of the end-effector is given by position \((p_{x}, p_{y})\) and the angle \(\phi\) w.r.t. \(x_{0}\). We want to use IK to find the joint variables \(\boldsymbol{q}=[\vartheta_{1}, \vartheta_{2}, \vartheta_{3}]\).

To achieve so, as shown in Fig. 35, we can first identify

(3)#\[ \phi=\vartheta_{1}+\vartheta_{2}+\vartheta_{3}\]

Also in Fig. 35, we can find the position of point \(W\) is

\[\begin{split}\begin{aligned} & p_{W x}=p_{x}-a_{3} c_{\phi}=a_{1} c_{1}+a_{2} c_{12} \\ & p_{W y}=p_{y}-a_{3} s_{\phi}=a_{1} s_{1}+a_{2} s_{12} \end{aligned}\end{split}\]

Applying cosine theorem to the triangle formed by \(a_{1}, a_{2}\) and the segment \(W-0\) gives

\[p_{W x}^{2}+p_{W y}^{2}=a_{1}^{2}+a_{2}^{2}-2 a_{1} a_{2} \cos \left(\pi-\vartheta_{2}\right) ;\]

Thus,

\[c_{2}=\frac{p_{W x}^{2}+p_{W y}^{2}-a_{1}^{2}-a_{2}^{2}}{2 a_{1} a_{2}}\]

For the existence of the triangle, it must be \(\sqrt{p_{W x}^{2}+p_{W y}^{2}} \leq a_{1}+a_{2}\). This condition is not met when the given end-effector pose is outside the arm reachable workspace.

\[\vartheta_{2}= \pm \cos ^{-1}\left(c_{2}\right)\]

Thus, two solution \(\vartheta_{2}\) are obtained, as shown in Fig. 36: the elbow-up pose when \(\vartheta_{2} \in(-\pi, 0)\); elbow-down pose when \(\vartheta_{2} \in(0, \pi)\).

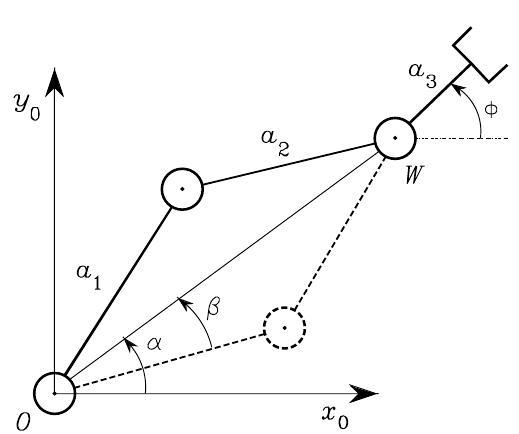
../_images/postures_2link_arm.jpg — Fig. 36 Admissible postures for a two-link planar arm#

To find \(\vartheta_{1}\)， consider the angles \(\alpha\) and \(\beta\) in Fig. 36. Notice that \(\alpha\) depends on the sign of \(p_{W x}\) and \(p_{W y}\); then,

\[\alpha=\operatorname{Atan} 2\left(p_{W y}, p_{W x}\right) .\]

To compute \(\beta\), applying again the cosine theorem yields

\[\beta=\cos ^{-1}\left(\frac{p_{W x}^{2}+p_{W y}^{2}+a_{1}^{2}-a_{2}^{2}}{2 a_{1} \sqrt{p_{W x}^{2}+p_{W y}^{2}}}\right)\]

with \(\beta \in(0, \pi)\) so as to preserve the existence of triangles. Then, it is

\[\vartheta_{1}=\alpha \pm \beta\]

where the positive sign holds for \(\vartheta_{2}<0\) and the negative sign for \(\vartheta_{2}>0\). Finally, \(\vartheta_{3}\) is computed from (3).

IK of Manipulators of Spherical Wrist#

Most of industrial robot arms are kinematically simple, the design is partly motivated by easing IK. In particular, a 6-DOF robot has closed-form IK if:

three consecutive revolute joint axes intersect at a common point, like for the spherical wrist; or
three consecutive revolute joint axes are parallel, like the three-link robot arm

Inspired by our above IK process to a three-link planar arm, an itermediate point \(W\) on the robot arm can be found, such that the IK can be decoupled into two lower-dimentional sub-problems. Specifically, for a robot arm with spherical wrist, a natural choice is to put \(W\) at the wrist position. As shown Fig. 37, if the end-effector pose is \(\boldsymbol{p}_{e}\) and \(\boldsymbol{R}_{e}=\left[\begin{array}{lll}\boldsymbol{n}_{e} & \boldsymbol{s}_{e} & \boldsymbol{a}_{e}\end{array}\right]\), the wrist position will be

\[\boldsymbol{p}_{W}=\boldsymbol{p}_{e}-d_{6} \boldsymbol{a}_{e}\]

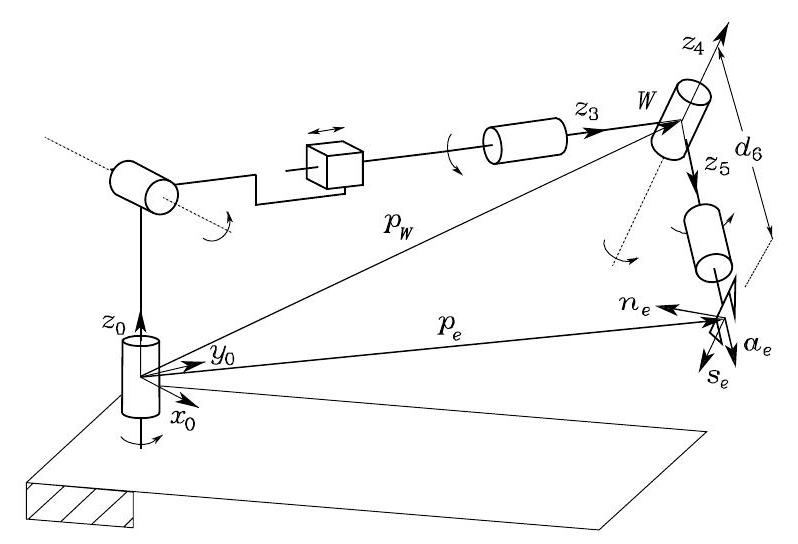
../_images/analytic_ik_decouple.jpg — Fig. 37 Robot arm with spherical wrist#

\(\boldsymbol{p}_{W}\) is a function of previous joint variables that determine the wrist position.

Hence, for a special 6-DOF robot arm with sphere wirst, IK can be solved by the following steps:

Compute the wrist position \(\boldsymbol{p}_{W}\left(q_{1}, q_{2}, q_{3}\right)\).
Solve inverse kinematics for \(\left(q_{1}, q_{2}, q_{3}\right)\).
Compute \(\boldsymbol{R}_{3}^{0}\left(q_{1}, q_{2}, q_{3}\right)\).
Compute \(\boldsymbol{R}_{e}^{3}\left(\vartheta_{4}, \vartheta_{5}, \vartheta_{6}\right)=\boldsymbol{R}_{3}^{0 T} \boldsymbol{R}_e\)
Solve inverse kinematics for orientation \(\left(\vartheta_{4}, \vartheta_{5}, \vartheta_{6}\right)\)

Therefore, IK is decoupled into: (1) IK for the arm (Step 1-2); and (2) the IK for the spherical wrist (Step 3-5).

Below are presented IK solutions for two types of arms (spherical and anthropomorphic) and IK solution for the spherical wrist.

IK for Spherical Arm#

Consider the spherical arm:

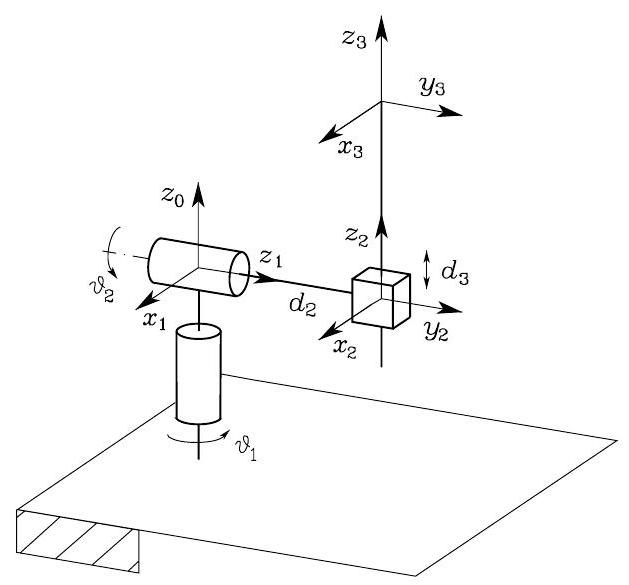
../_images/spherical_arm1.jpg — Fig. 38 Spherical arm#

Its FK is

\[\begin{split} \boldsymbol{T}_{3}^{0}(\boldsymbol{q})=\boldsymbol{T}_{1}^{0} \boldsymbol{T}_{2}^{1} \boldsymbol{T}_{3}^{2}=\left[\begin{array}{cccc} c_{1} c_{2} & -s_{1} & c_{1} s_{2} & c_{1} s_{2} d_{3}-s_{1} d_{2} \\ s_{1} c_{2} & c_{1} & s_{1} s_{2} & s_{1} s_{2} d_{3}+c_{1} d_{2} \\ -s_{2} & 0 & c_{2} & c_{2} d_{3} \\ 0 & 0 & 0 & 1 \end{array}\right] \end{split}\]

To solve IK for the joint variables \(\vartheta_{1}, \vartheta_{2}, d_{3}\) given \(\boldsymbol{p}_{W}=[p_{Wx}, p_{Wy}, p_{Wz}]^T\), just equate \(\boldsymbol{p}_{W}\) to the first three elements of the fourth columns. This leads to the following (after some manipulation)

\[\begin{split}\left[\begin{array}{c} p_{W x} c_{1}+p_{W y} s_{1} \\ -p_{W z} \\ -p_{W x} s_{1}+p_{W y} c_{1} \end{array}\right]=\left[\begin{array}{c} d_{3} s_{2} \\ -d_{3} c_{2} \\ d_{2} \end{array}\right]\end{split}\]

Then, solving the above equation for \(\vartheta_{1}, \vartheta_{2}, d_{3}\) yields

\[\vartheta_{1}=2 \operatorname{Atan} 2\left(-p_{W x} \pm \sqrt{p_{W x}^{2}+p_{W y}^{2}-d_{2}^{2}}, d_{2}+p_{W y}\right)\]

\[\vartheta_{2}=\operatorname{Atan} 2\left(p_{W x} c_{1}+p_{W y} s_{1}, p_{W z}\right)\]

\[d_{3}=\sqrt{\left(p_{W x} c_{1}+p_{W y} s_{1}\right)^{2}+p_{W z}^{2}}\]

IK of Anthropomorphic Arm#

Consider the anthropomorphic arm:

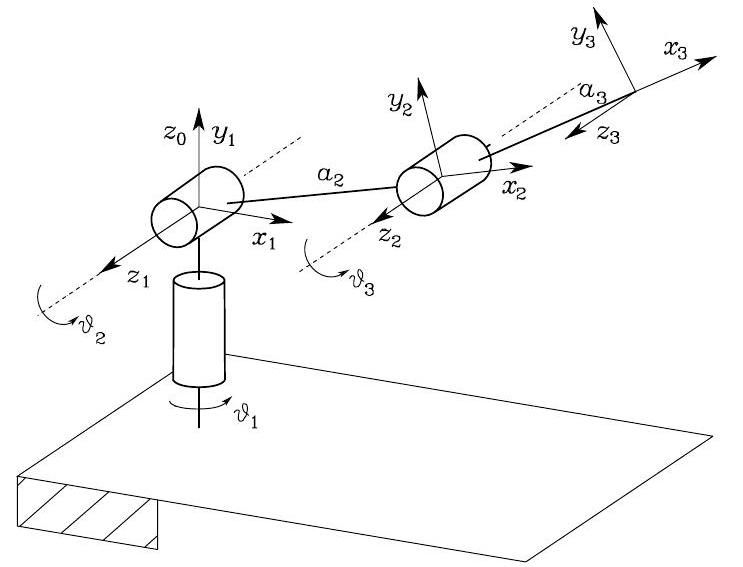
../_images/anthropomorphic_arm1.jpg — Fig. 39 Anthropomorphic arm#

\[\begin{split}\boldsymbol{T}_{3}^{0}(\boldsymbol{q})=\boldsymbol{T}_{1}^{0} \boldsymbol{T}_{2}^{1} \boldsymbol{T}_{3}^{2}=\left[\begin{array}{cccc} c_{1} c_{23} & -c_{1} s_{23} & s_{1} & c_{1}\left(a_{2} c_{2}+a_{3} c_{23}\right) \\ s_{1} c_{23} & -s_{1} s_{23} & -c_{1} & s_{1}\left(a_{2} c_{2}+a_{3} c_{23}\right) \\ s_{23} & c_{23} & 0 & a_{2} s_{2}+a_{3} s_{23} \\ 0 & 0 & 0 & 1 \end{array}\right]\end{split}\]

To find the joint variables \(\vartheta_{1}, \vartheta_{2}, d_{3}\) corresponding to \(\boldsymbol{p}_{W}=[p_{Wx}, p_{Wy}, p_{Wz}]^T\), we equate the first three elements of the fourth columns of the matrix

\[\begin{split}\begin{aligned} & p_{W x}=c_{1}\left(a_{2} c_{2}+a_{3} c_{23}\right) \\ & p_{W y}=s_{1}\left(a_{2} c_{2}+a_{3} c_{23}\right) \\ & p_{W z}=a_{2} s_{2}+a_{3} s_{23} . \end{aligned}\end{split}\]

There exist four solutions:

\[\left(\vartheta_{1, \mathrm{I}}, \vartheta_{2, \mathrm{I}}, \vartheta_{3, \mathrm{I}}\right) \quad\left(\vartheta_{1, \mathrm{I}}, \vartheta_{2, \mathrm{III}}, \vartheta_{3, \mathrm{II}}\right) \quad\left(\vartheta_{1, \mathrm{II}}, \vartheta_{2, \mathrm{II}}, \vartheta_{3, \mathrm{I}}\right) \quad\left(\vartheta_{1, \mathrm{II}}, \vartheta_{2, \mathrm{IV}}, \vartheta_{3, \mathrm{II}}\right)\]

with

\[\begin{split}\begin{aligned} \vartheta_{3, \mathbf{I}}&=\operatorname{Atan} 2 \left( s_3^{+}, c_{3}\right)\\ \vartheta_{3, \mathrm{II}} & =\operatorname{Atan} 2 \left( s_3^{-}, c_{3}\right) \end{aligned}\end{split}\]

\[\begin{split}\begin{aligned} \vartheta_{1, \mathrm{I}} & =\operatorname{Atan} 2\left(p_{W y}, p_{W x}\right) \\ \vartheta_{1, \mathrm{II}} & =\operatorname{Atan} 2\left(-p_{W y},-p_{W x}\right) . \end{aligned}\end{split}\]

\[\begin{split}\begin{aligned} \vartheta_{2, \mathrm{I}}=\operatorname{Atan} 2 & \left(\left(a_{2}+a_{3} c_{3}\right) p_{W z}-a_{3} s_{3}^{+} \sqrt{p_{W x}^{2}+p_{W y}^{2}},\right. \left.\left(a_{2}+a_{3} c_{3}\right) \sqrt{p_{W x}^{2}+p_{W y}^{2}}+a_{3} s_{3}^{+} p_{W z}\right) \\ \vartheta_{2, \mathrm{II}}=\operatorname{Atan} 2 & \left(a_{2}+a_{3} c_{3}\right) p_{W z}+a_{3} s_{3}^{+} \sqrt{p_{W x}^{2}+p_{W y}^{2}}, \left.-\left(a_{2}+a_{3} c_{3}\right) \sqrt{p_{W x}^{2}+p_{W y}^{2}}+a_{3} s_{3}^{+} p_{W z}\right) \end{aligned}\end{split}\]

\[\begin{split}\begin{aligned} \vartheta_{2, \mathrm{III}}=\operatorname{Atan2} & \left(\left(a_{2}+a_{3} c_{3}\right) p_{W z}-a_{3} s_{3}^{-} \sqrt{p_{W x}^{2}+p_{W y}^{2}},\right. \left.\left(a_{2}+a_{3} c_{3}\right) \sqrt{p_{W x}^{2}+p_{W y}^{2}}+a_{3} s_{3}^{-} p_{W z}\right) \\ \vartheta_{2, \mathrm{IV}}=\operatorname{Atan} 2 & \left(\left(a_{2}+a_{3} c_{3}\right) p_{W z}+a_{3} s_{3}^{-} \sqrt{p_{W x}^{2}+p_{W y}^{2}},\right. \left.-\left(a_{2}+a_{3} c_{3}\right) \sqrt{p_{W x}^{2}+p_{W y}^{2}}+a_{3} s_{3}^{-} p_{W z}\right) \end{aligned}\end{split}\]

\[c_{3}=\frac{p_{W x}^{2}+p_{W y}^{2}+p_{W z}^{2}-a_{2}^{2}-a_{3}^{2}}{2 a_{2} a_{3}}\]

\[s_{3}^+= \sqrt{1-c_{3}^{2}}\quad\quad s_{3}^-= -\sqrt{1-c_{3}^{2}}\]

The four solutions are illustrated below: shoulder-right/elbow-up, shoulder-left/elbowup, shoulder-right/elbow-down, shoulder-left/elbow-down; obviously, the forearm orientation is different for the two pairs of solutions.

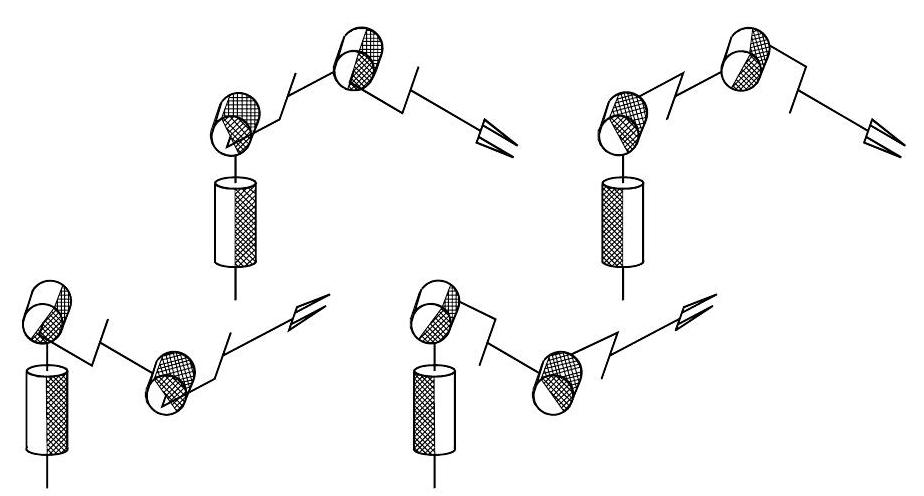
../_images/4IK_solutions_anthropomorphic_arm.jpg — Fig. 40 The four configurations of an anthropomorphic arm compatible with a given wrist position#

IK of Spherical Wrist#

Consider the spherical wrist below.

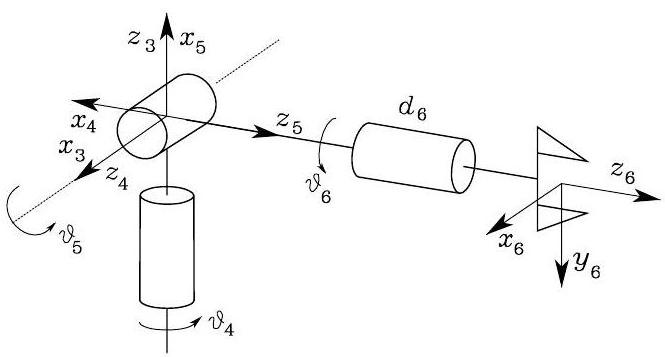
../_images/spherical_wrist1.jpg — Fig. 41 Spherical wrist#

To find the joint variables \(\vartheta_{4}, \vartheta_{5}, \vartheta_{6}\) corresponding to a given end-effector orientation \(\boldsymbol{R}_{6}^{3}\). As previously pointed out, these angles constitute a set of Euler angles ZYZ with respect to Frame 3.

\[\begin{split}\boldsymbol{R}_{6}^{3}=\left[\begin{array}{rrr} n_{x}^{3} & s_{x}^{3} & a_{x}^{3} \\ n_{y}^{3} & s_{y}^{3} & a_{y}^{3} \\ n_{z}^{3} & s_{z}^{3} & a_{z}^{3} \end{array}\right]\end{split}\]

from its expression in terms of the joint variables, it is possible to compute

\[\begin{split}\begin{aligned} & \vartheta_{4}=\operatorname{Atan} 2\left(a_{y}^{3}, a_{x}^{3}\right) \\ & \vartheta_{5}=\operatorname{Atan} 2\left(\sqrt{\left(a_{x}^{3}\right)^{2}+\left(a_{y}^{3}\right)^{2}}, a_{z}^{3}\right) \\ & \vartheta_{6}=\operatorname{Atan} 2\left(s_{z}^{3},-n_{z}^{3}\right) \end{aligned}\end{split}\]

for \(\vartheta_{5} \in(0, \pi)\), and

\[\begin{split}\begin{aligned} & \vartheta_{4}=\operatorname{Atan} 2\left(-a_{y}^{3},-a_{x}^{3}\right) \\ & \vartheta_{5}=\operatorname{Atan} 2\left(-\sqrt{\left(a_{x}^{3}\right)^{2}+\left(a_{y}^{3}\right)^{2}}, a_{z}^{3}\right) \\ & \vartheta_{6}=\operatorname{Atan} 2\left(-s_{z}^{3}, n_{z}^{3}\right) \end{aligned}\end{split}\]

for \(\vartheta_{5} \in(-\pi, 0)\)