Robot Configuration

Robot Configuration#

../_images/robotarm.png

Fig. 1 Franka research robot arm#

A robot manipulator is mechanically constructed by

  • a set of rigid bodies, each body called a link,

  • joints, connecting two consecutive links and providing motion constraints (degrees of freedom)

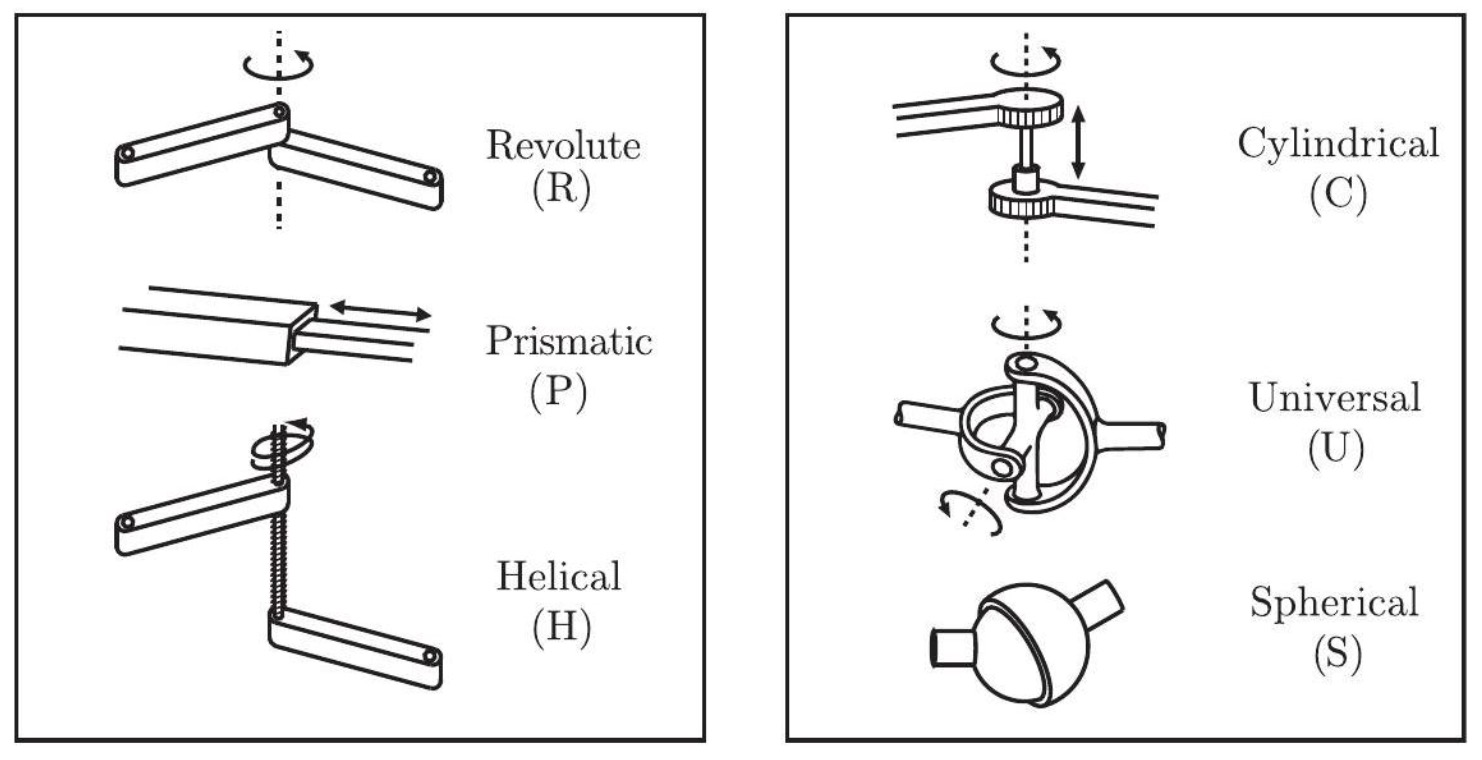
    ../_images/joints.png

    Fig. 2 Different type of joints#

  • actuators, such as electric/hydraulic/pneumatic actuators, deliver forces or torques that cause the robot’s links to move,

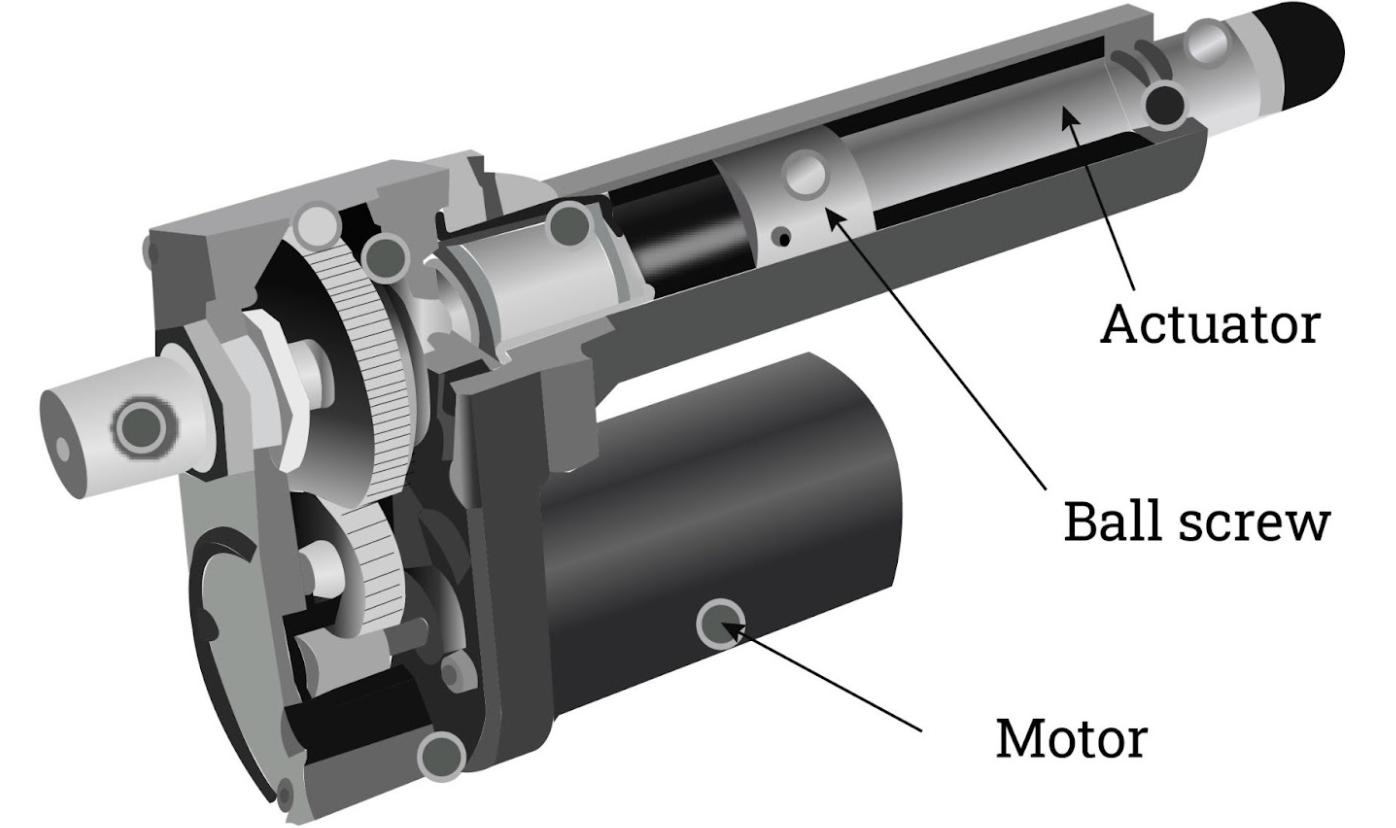
    ../_images/electric_actuator.png

    Fig. 3 Electric actuators#

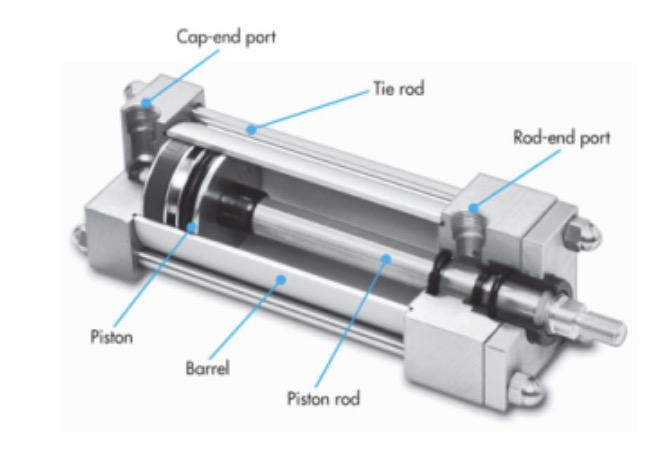
    ../_images/hydralic_actuator.png

    Fig. 4 Hydralic actuator#

  • an end effector, such as a gripper or hand, is attached to a specific link for specific tasks.

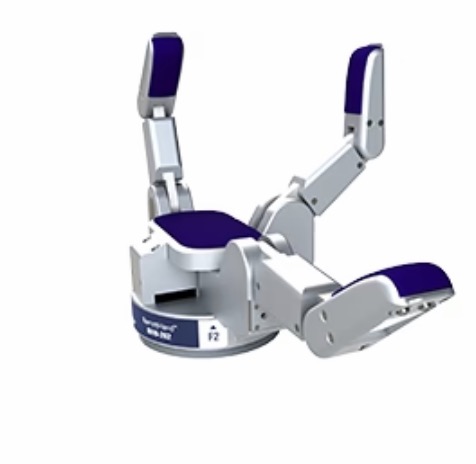
    ../_images/endeffector1.jpg

    Fig. 5 The Barrett Hand#

    ../_images/endeffector2.png

    Fig. 6 The Shadow Hand#

The typical structure of a robot arm is an open kinematic chain. From a topological viewpoint, a kinematic chain is open when there is only one sequence of links connecting the two ends of the chain. Alternatively, kinematic chain is closed when a sequence of links forms a loop.

Configuration#

Important

The configuration of a robot is a complete specification of the position of every point of the robot. Since a robot’s links are rigid and of a known shape, only a few variables (coordinates in a general sense) are needed to represent its configuration.

For example, in the following figure, the configuration of a door can be represented by the hinge angle \(\theta\). The configuration of a point on a plane can be represented by two coordinates, \((x, y)\). The configuration of a coin lying heads up on a flat table can be represented by three coordinates: \((x, y)\) that specifies the location of a particular point on the coin, and \((\theta)\) that specifies the coin’s orientation.

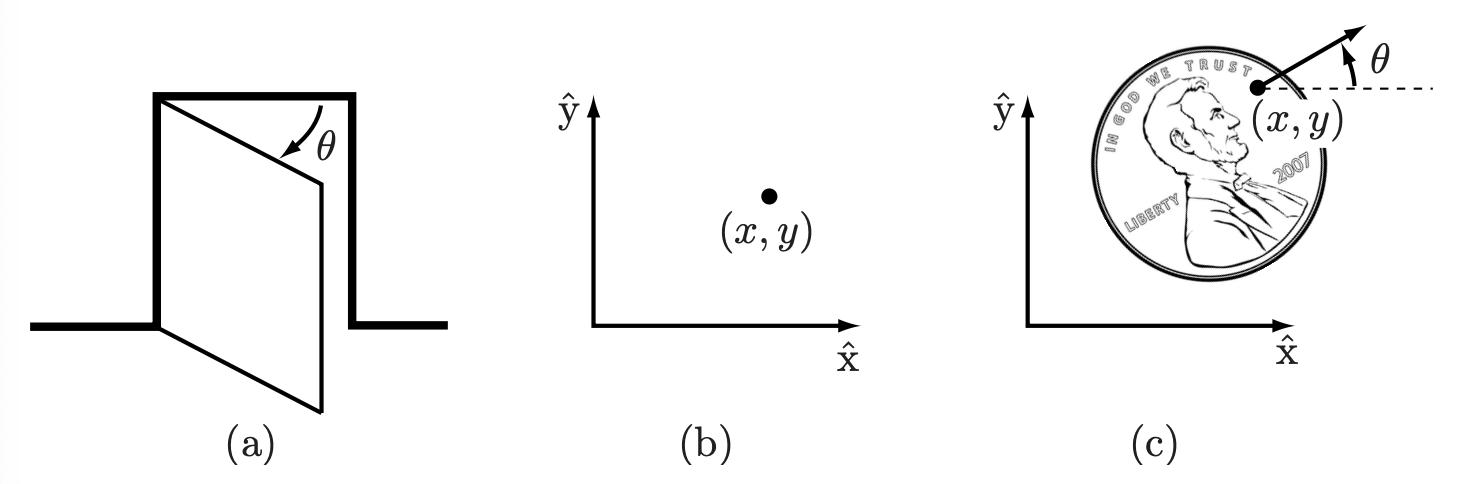
../_images/examples.png

Fig. 7 (a) The configuration of a door is represented by the angle \(\theta\). (b) The configuration of a point in a plane is represented by coordinates \((x, y)\). (c) The configuration of a coin (heads up) on a table is represented by \((x, y, \theta)\).#

Degrees of Freedom#

Important

The minimum number \(n\) of coordinates needed to represent the configuration of a robot is the number of degrees of freedom (dof). The \(n\)-dimensional space containing all possible configurations of a robot is called the configuration space (C-space). The configuration of a robot is represented by a point in its C-space.

General Rule#

We have the following general rule to determine the number of dof of a robot:

Important

degrees of freedom = number of variables - number of independent constraints

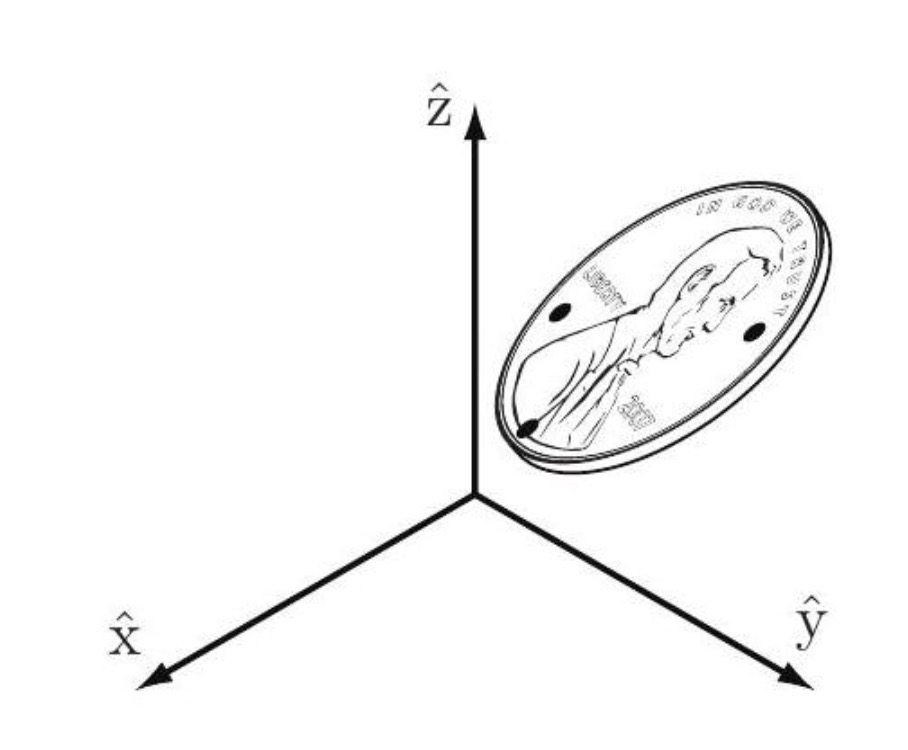
../_images/coin.png

Fig. 8 A coin in 3D space#

Example: consider a coin in 3D space in Fig. 8, the coordinates for the three points \(A, B\), and \(C\) are given by \(\left(x_{A}, y_{A}, z_{A}\right),\left(x_{B}, y_{B}, z_{B}\right)\), and \(\left(x_{C}, y_{C}, z_{C}\right)\), respectively. Point \(A\) can be placed freely (three degrees of freedom). The location of point \(B\) is subject to the constraint \(d(A, B)=d_{A B}\), meaning it must lie on the sphere of radius \(d_{A B}\) centered at \(A\). Thus we have \(3-1=2\) freedoms to specify, which can be expressed as the latitude and longitude for the point on the sphere. Finally, the location of point \(C\) must lie at the intersection of spheres centered at \(A\) and \(B\) of radius \(d_{A C}\) and \(d_{B C}\), respectively. In the general case the intersection of two spheres is a circle, and the location of point \(C\) can be described by an angle that parametrizes this circle. Point \(C\) therefore adds \(3-2=1\) freedom. Once the position of point \(C\) is chosen, the coin is fixed in space. In summary, a rigid body in three-dimensional space has six freedoms, which can be described by the three coordinates parametrizing point \(A\), the two angles parametrizing point \(B\), and one angle parametrizing point \(C\), provided \(A, B\), and \(C\) are noncollinear.

  • A rigid body moving in 3-dimensional space has 6 degrees of freedom.

  • A rigid body moving in a 2-dimensional plane has 3 degrees of freedom.

DOF of Different Joint Types#

In a robot, a joint can be viewed as providing freedoms to allow one rigid body to move relative to another. It can also be viewed as providing constraints on the possible motions of the two rigid bodies it connects. The following table summarizes the freedoms and constraints provided by the various joint types.

Joint type

dof

# of constraints between two bodies in 3D space

Revolute (R)

1

5

Prismatic (P)

1

5

Helical (H)

1

5

Cylindrical (C)

2

4

Universal (U)

2

4

Spherical (S)

3

3

Grübler’s Formula#

Important

Consider a mechanism consisting of \(L\) links, where the ground is also regarded as a link. Let \(J\) be the number of joints, \(m\) be the number of degrees of freedom of a rigid body (\(m=3\) for planar mechanisms and \(m=6\) for 3D mechanisms), \(f_{i}\) be the number of freedoms provided by joint \(i\), and \(c_{i}\) be the number of constraints provided by joint \(i\), where \(f_{i}+c_{i}=m\) for all \(i\). Then the Grübler’s formula for degrees of freedom of the mechanism is

\[\begin{split}\begin{aligned} \operatorname{dof} & =\underbrace{m(L-1)}_{\text {total number of freedoms for all rigid bodies }}-\underbrace{\sum_{i=1}^{J} c_{i}}_{\text {joint constraints }} \\ & =m(L-1)-\sum_{i=1}^{J}\left(m-f_{i}\right) \\ & =m(L-1-J)+\sum_{i=1}^{J} f_{i} . \end{aligned}\end{split}\]

This formula holds only if all joint constraints are independent. If they are not independent then the formula provides a lower bound on the number of degrees of freedom.

Below are some examples of using Grubler’s Formula to find the DoFs of different machenisms.

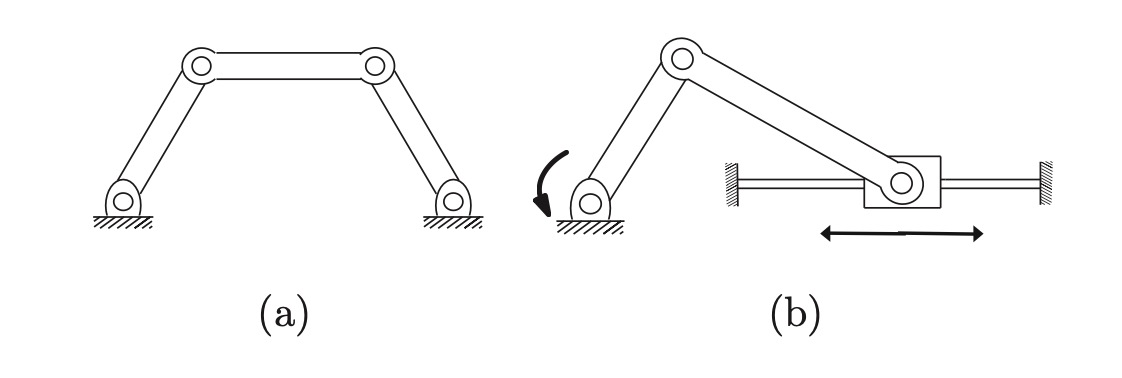
../_images/gf_example1.png

Fig. 9 (a) Four-bar linkage and (b) Slider-crank mechanism.#

(Four-bar linkage): \(L=4, J=4\), and \(f_{i}=1, i=1, \ldots, 4\). Thus, \(\operatorname{dof}\)=1.
Slider-crank: \(L=4\), \(J=4,\) and \(f_{i}=1, i=1, \ldots, 4\). Thus, \(\operatorname{dof}\)=1.

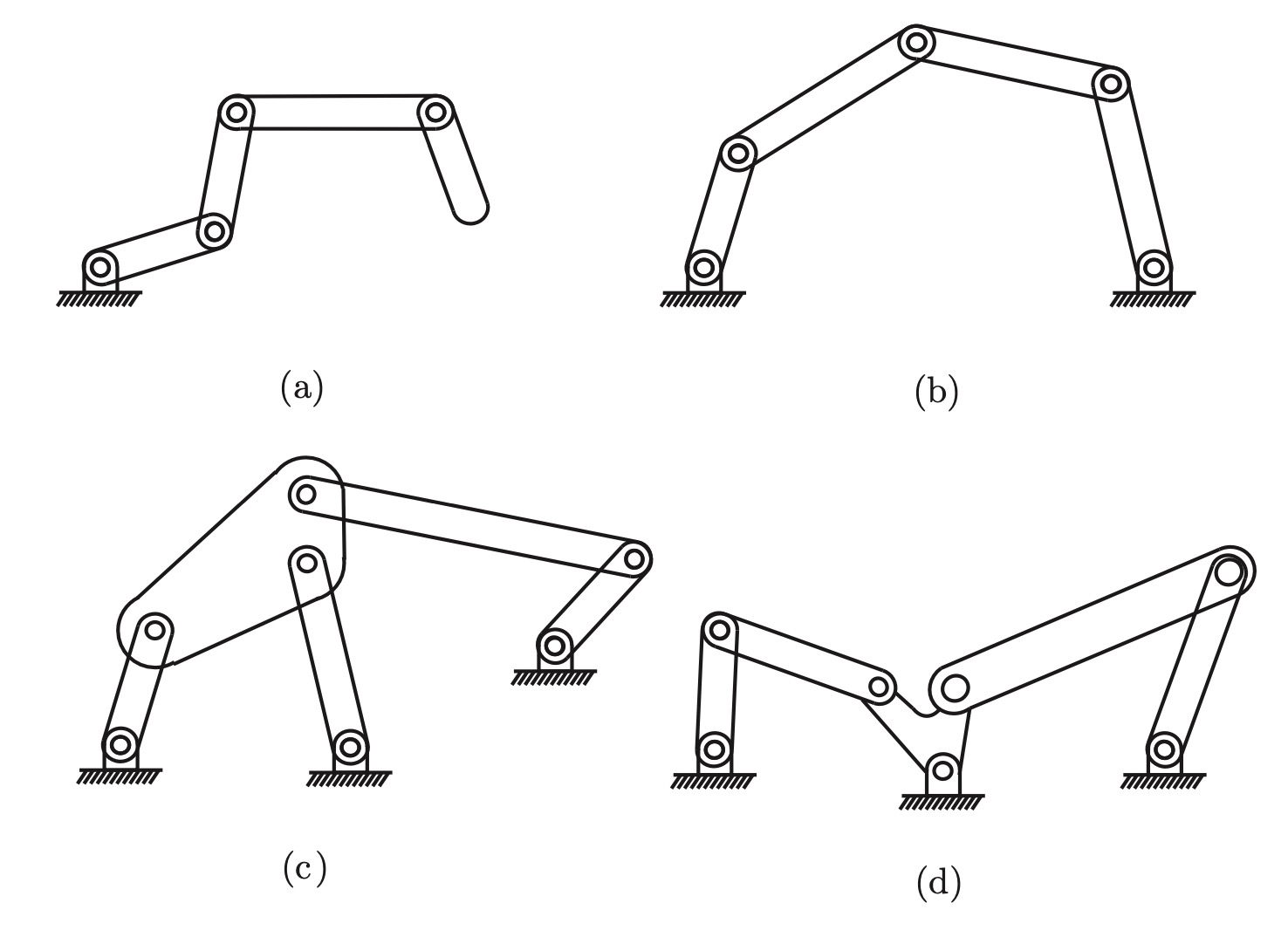
../_images/gf_example2.png

Fig. 10 (a) \(k\)-link planar serial chain. (b) Five-bar planar linkage. (c) Stephenson six-bar linkage. (d) Watt six-bar linkage.#

The \(k\)-link planar robot: \(L=k+1\), \(J=k\), \(f_{i}=1\) for all \(i\). Thus, \(\operatorname{dof}=3*((k+1)-1-k)+k=k\).
The five-bar linkage: \(L=5\), \(J=5\), each \(f_{i}=1\). Therefore, \(\operatorname{dof}=3*(5-1-5)+5=2\).
Stephenson six-bar linkage: \(L=6, J=7\), and \(f_{i}=1\) for all \(i\). Therefore, \(\operatorname{dof}=3*(6-1-7)+7=1\).
Watt six-bar linkage: \(L=6, J=7\), and \(f_{i}=1\) for all \(i\). Therefore, \(\operatorname{dof}=3*(6-1-7)+7=1\).

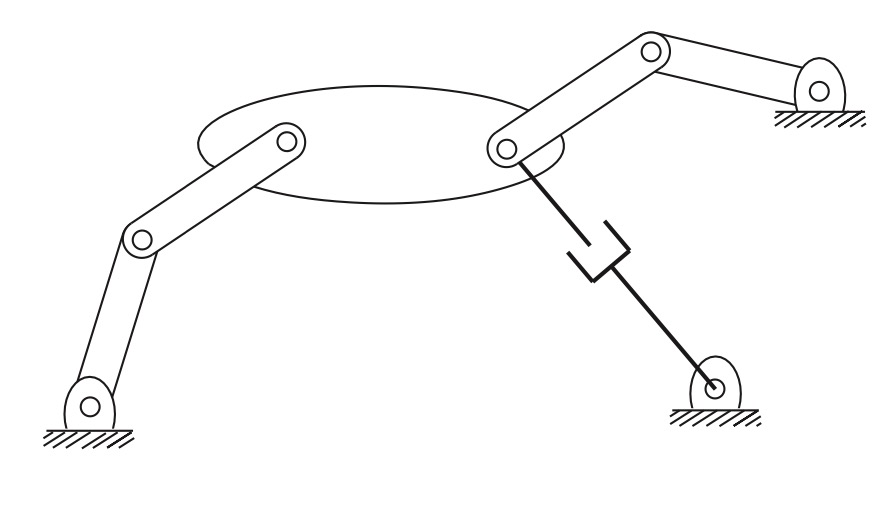
../_images/gf_example3.png

Fig. 11 A planar mechanism with two overlapping joints.#

The planar mechanism in Fig. 11 has three links that meet at a single point on the right of the large link. Recalling that a joint by definition connects exactly two links, the joint at this point should not be regarded as a single revolute joint. Rather, it should be counted as two revolute joints overlapping each other. The mechanism consists of eight links \((L=8)\), 8 revolute joints, and 1 prismatic joint. The Grübler’s formula:

\[\operatorname{dof}=3*(8-1-9)+9*(1)=3\]
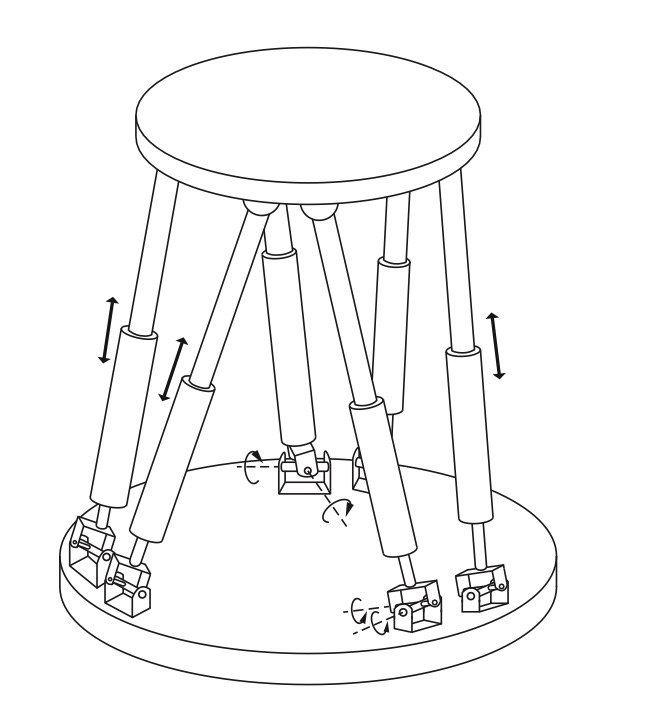
../_images/gf_example4.png

Fig. 12 Stewart-Gough platform#

The Stewart-Gough platform consists of two platforms - the lower one is regarded as ground, the upper one mobile - connected by six universal-prismatic-spherical (UPS) legs. The total number of links is \(14(L=14)\). There are six universal joints (for each, \(f_{i}=2\) ), six prismatic joints (for each, \(f_{i}=1\) ), and six spherical joints (for each, \(f_{i}=3\) ). The total number of joints is 18 . Using Grübler’s formula, we have

\[\operatorname{dof}=6*(14-1-18)+6*(1)+6*(2)+6*(3)=6 .\]

Workspace of Robot Arms#

The workspace is the space of the environment a robot arm’s end-effector can access. Its shape and volume depend on the robot arm’s structure as well as mechanical joint limits. The workspace is independent of the task. In the following, below is the workspace of different commonly used robot arms.

Cartesian robot arm includes three prismatic joints whose axes typically are mutually orthogonal.

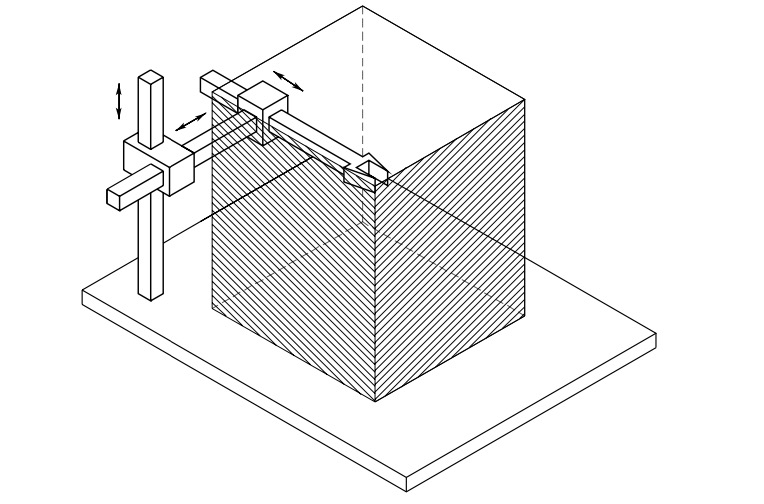
../_images/cartesian_robot.jpg

Fig. 13 Cartesian robot arm and its workspace#

Cylindrical robot arm differs from Cartesian in that the first prismatic joint is replaced with a revolute joint.

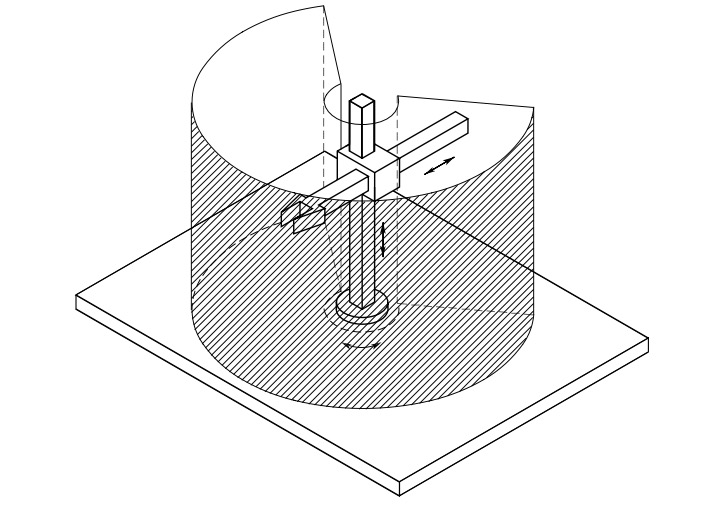
../_images/cylindrical_robot.jpg

Fig. 14 Cylindrical robot arm and its workspace#

Spherical robot arm differs from cylindrical in that the 2nd prismatic joint is replaced with a revolute joint.

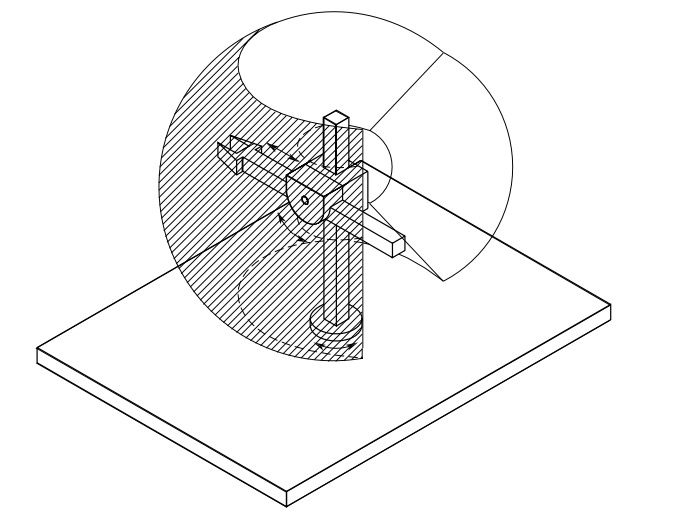
../_images/spherical_robot.jpg

Fig. 15 Spherical robot arm and its workspace#

A special robot arm is SCARA robot arm, which has the feature that all the axes of motion are parallel.

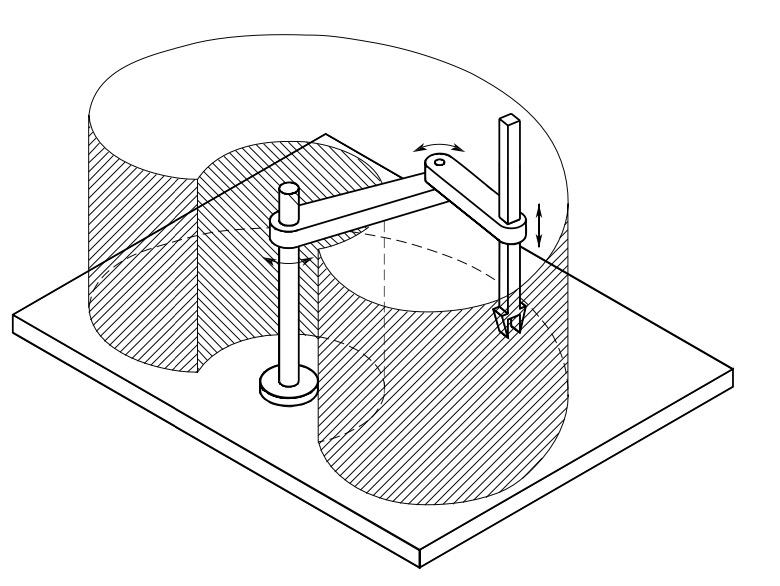
../_images/SCARA_robot.jpg

Fig. 16 SCARA robot arm and its workspace#

Anthropomorphic robot arm has three revolute joints; the revolute axis of the first joint is orthogonal to the axes of the other two which are parallel.

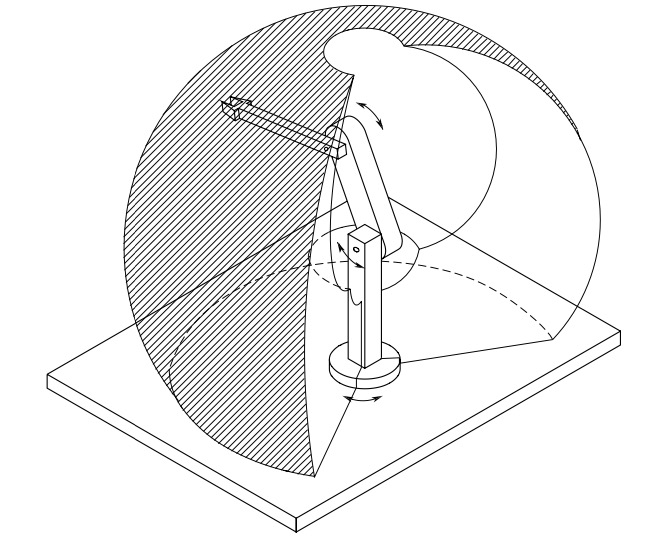
../_images/anthropomophic_robot.jpg

Fig. 17 Anthropomorphic robot arm and its workspace#