Overview of Robot Arm Control#
The control of a robot arm is to determine the time sequence of control inputs (i.e., joint torques) to achieve a specified task. In many robotics tasks, the task is specified usually in the operational space (such as end-effector motion and forces), whereas control inputs (joint torque) is usually made in the joint space. There are two control schemes: joint space control and operational space control. In both schemes, the control diagram is closed-loops
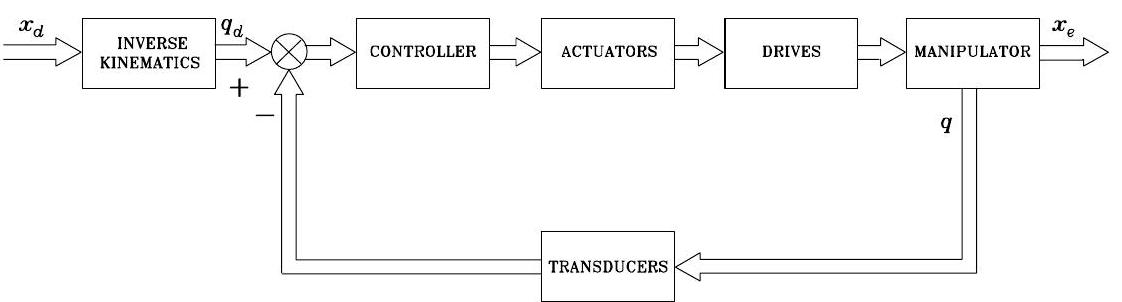
Joint space control#
The joint space control is shown in joint_control222. Here, inverse kinematics is
use to convert the specified end-effector motion
\(\boldsymbol{x}_{d}\) to the desired joint motion
\(\boldsymbol{q}_{d}\). Then, a joint space controller
is designed to allow the actual joint value \(\boldsymbol{q}\) to
track \(\boldsymbol{q}_{d}\). As you can see, the controller directly
regulates the joint tracking error \(\boldsymbol{q}_{d}-\boldsymbol{q}_{}\), instead of operational space error \(\boldsymbol{x}_{d}-\boldsymbol{x}_{e}\). Thus, the end-effector pose
\(\boldsymbol{x}_{e}\) is controlled in an open-loop fashion (instead, \(\boldsymbol{q}_{}\) is controlled in closed-loop way). This can lead to operational space control error if IK has some error.
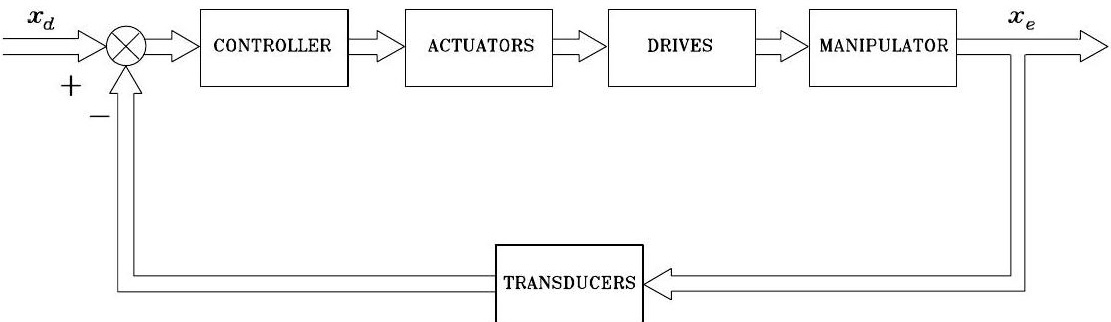
Operational space control#
The operational space control is shown in operational_space_control222.
Here, the operational space motion \(\boldsymbol{x}_{e}\) is directly fed back
to the controller. Thus, it addresses the drawbacks of joint space
control. However, the control algorithm typically is more complex in design and it requires measuring the operational space motion
\(\boldsymbol{x}_{e}\), which is typically challenging.
Modeling Joint Motors#
According to the previous lecture, the dynamics equation of a robot arm only with joint input torque \(\boldsymbol{\tau}\) is:

Transmission between motor and joint#
Joint-Motor Transmission#
As shown in motori_kinematics, let \(\boldsymbol{q}_{m}=[\theta_{m1}, \theta_{m2}, ...\theta_{mn}]^T\)
be the vector of joint motor angles. The transmissions - assumed to be
rigid and with no backlash - between the motor and joint motion is
where \(\boldsymbol{K}_{r}=\text{diag}(k_{r_1}, k_{r_2}, ..., k_{r_n})\) is a diagonal joint-motor transmission matrix, and each diagonal element \(k_{r_i}\) is the gear ratio of joint \(i\) is, typically much greater than identity. Let \(\boldsymbol{\tau}_{m}=[\tau_{m1},\tau_{m2},...,,\tau_{mn}]^T\) denote the vector of all motor torques. Based on principle of virtual work, one has the following transmission between motor torque and joint input torque:
Electric Motor Model#
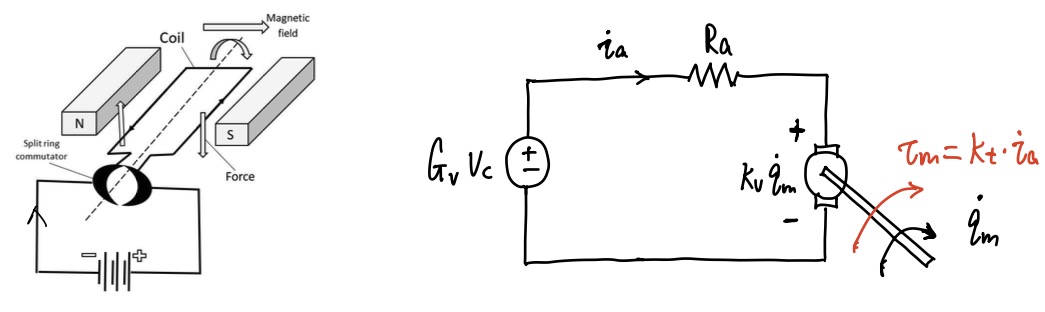
Direct current motor circuit#
For a direct current (DC) motor motor_circuit, we have the following model:
Here, \(\boldsymbol{K}_{t}\) is the torque constants; \(\boldsymbol{i}_{a}\) is the armature currents; \(\boldsymbol{v}_{a}\) is the vector of armature voltages; \(\boldsymbol{R}_{a}\) is the armature resistances; \(\boldsymbol{K}_{v}\) is the back electromotive force (EMF) constants; \(\boldsymbol{G}_{v}\) is the voltage amplifiers; and \(\boldsymbol{v}_{c}\) is the voltages of the servomotors.
which gives a relationship between the applied motor voltage \(\boldsymbol{v}_c\), the motor-generated joint torque \(\boldsymbol{\tau}\), and the joint velocity \(\boldsymbol{\dot{q}}\).
When we consider the robot arm system joining the DC motor () and robot arm own dynamics (),
overall diagram is shown in voltage_control.
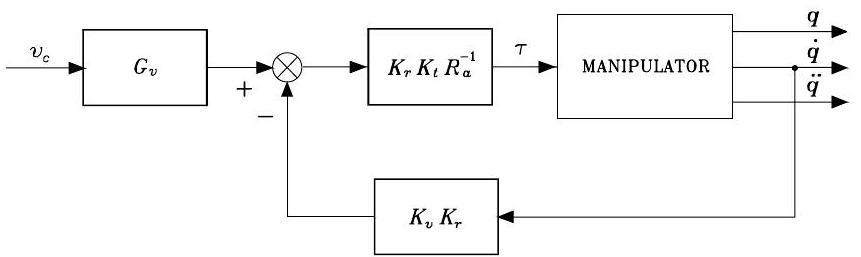
The entire system joining DC motor and robot arm.#
“Robot arm is an Integrator”#
If the following assumptions hold for ():
the joint-motor transmission value \(\boldsymbol{K}_{r}\) is much greater than unity;
the motor resistance \(\boldsymbol{R}_{a}\) is very small, which is the case for high-efficiency servomotors;
the joint torques value \(\boldsymbol{\tau}\) needed for the operation of the robot arm not too large (light robot arm);
then, () can be approximated to
further
() says, under the above-stated assumptions, the robot arm system, i.e., DC motor plus arm, can be considered as a voltage-to-velocity system: the joint velocity of the robot arm is linear to the voltage input to the servomotor. In other words, the robot arm system can be considered as an integrator!
The benefit of () is that it is a decentralized control system (each joint can be controlled independently of the others): the velocity of the \(i\)-th joint depends only on the \(i\)-th voltage input, since the matrix \(\boldsymbol{G}_{v}^{-1} \boldsymbol{K}_{v} \boldsymbol{K}_{r}\) is diagonal.
General case: Torque-Controlled System#
If the assumption in the above section does not hold, for example, when \(\boldsymbol{K}_{r}=\boldsymbol{I}\), we do not have such a nice property of “robot arm as an integrator”, and then the robot will exhibit complex eletro-mechnical dynamics. How do we control the robot arm??
Well, from (), we still have the following relation between the motor-generated joint torque and armature current
i.e.,
Thus, in reality, we have a local feedback control system inside the motor to regulate the armature current \(\boldsymbol{i}_a\). This local control system will establish the following relationship between the motor voltage input and the armature current:
Therefore, based on () and (), we have
The above equation says that, in the general case, the whole system, i.e., DC motor plus robot arm, can be considered as a voltage-to-torque system: you can directly regulate the joint torque of a robot arm by regulating the voltage to the servomotor.
