Velocity Kinematics#
Derivative of Rotation#
Consider a time-varying rotation matrix \(\boldsymbol{R}=\boldsymbol{R}(t)\). Based on the property of rotation matrix, we always have
Differentiating the above equation with respect to time gives
Let’s define a new matrix
Then, the above equation becomes
Any matrix that satisfies the above equation is called skew-symmetric matrix (a square matrix whose transpose equals its negative). From (4), we have
Now, let’s find out what is \(\boldsymbol{S}\) and its physics interpretation.
Suppose \({\boldsymbol{R}}\) represents a rotation of a moving body frame \(O'-x'y'z'\) with respect to a fixed reference frame \(O-xyz\). Let’s consider a point \(P\), rigidly fixed to the body frame (thus moving as body is moving), with its body frame coordinate \(\boldsymbol{p}^{\prime}\). Then, its coordinate in the reference frame \(\boldsymbol{p}\) is
which is time varying.
Taking the derivative to both sides of (6) yields
where we have used (4).
Recall in your mechanics courses, given the angular velocity \(\boldsymbol{\omega}\) of a moving body with respect to a reference frame, any point \(P\) fixed on this body has a velocity in the reference frame as
where \(\boldsymbol{\omega}=\left[\begin{array}{lll}\omega_{x} & \omega_{y} & \omega_{z}\end{array}\right]^{T}\) is the angular velocity of the moving body, expressed in the reference frame.
If we look at and compare (7) and (8), we can find
Thus, this skew-symmetric matrix \(\boldsymbol{S}\) can be obtained directly from the body’s angular velocity \(\boldsymbol{\omega}\). We typically write it as \(\boldsymbol{S}(\boldsymbol{\omega})\).
In sum, we can conclude the derivative of a rotation matrix is
Note that the above angular velocity \(\boldsymbol{\omega}\) is expressed in the reference frame! (not in the body frame)
One property of \(\boldsymbol{S}(\boldsymbol{\omega})\): For any rotation matrix \(\boldsymbol{R}\), one has
Derivative of Rotation + Translation#
Consider a transformation mapping the coordinate mapping of a point \(P\) (NOT necessarily fixed on a moving body) from the body frame \(O_1-x_1y_1z_1\) to reference frame \(O_0-x_0y_0z_0\)
Differentiating the above equation with respect to time yields
In the above (10), because point \(P\) is not necessarily fixed on the body, and it may have its local movement in the body frame with the local velocity \(\dot{{\boldsymbol{p}}}^{1}\). Special care should be paied to the notation of \(\dot{{\boldsymbol{p}}}^{1}\): \(\dot{{\boldsymbol{p}}}^{1}\) is purely taking the derivative to xyz body coordinate instead of body xyz axises.
Since \(\boldsymbol{R}_{1}^{0} \boldsymbol{p}^{1}=\boldsymbol{p}^{0}\) and \(\boldsymbol{S}\left(\boldsymbol{\omega}_{1}^{0}\right)=[\omega_{1}^{0} \times] \), the above equation (10) becomes
Here are some explaination of each term on the right side of (11):
\(\dot{\boldsymbol{o}}_{1}^{0}\) is the contribution to point \(P\)’s total velocity (in reference frame) by the translation of body frame.
\(\boldsymbol{R}_{1}^{0} \dot{\boldsymbol{p}}^{1}\) is the contribution to point \(P\)’s total velocity (in reference frame) by the local movement of \(P\) on the body frame. Here, \(\dot{\boldsymbol{p}}^{1}\) is the local velocity in the body frame, and \(\boldsymbol{R}_{1}^{0} \dot{\boldsymbol{p}}^{1}\) is the transformed local velocity to the reference frame.
\(\boldsymbol{S}\left(\boldsymbol{\omega}_{1}^{0}\right) \boldsymbol{R}_{1}^{0} \boldsymbol{p}^{1}=\omega_{1}^{0} \times \boldsymbol{p}^{0}\) is the contribution to point \(P\)’s total velocity by the rotation of the body frame.
Notice that, if \(\boldsymbol{p}^{1}\) is fixed in the moving body frame , then (11) can be further reduced to
Apply to links of a robot arm#
Consider the Link \(i\) of a robot arm in Fig. 54. We can apply DH convention to find the transformation between Frame \(i-1\) (attached to link \(i-1\)) and Frame \(i\) (attached to this link \(i\)). Next, we find out what the relationship between the velocity of those two links.
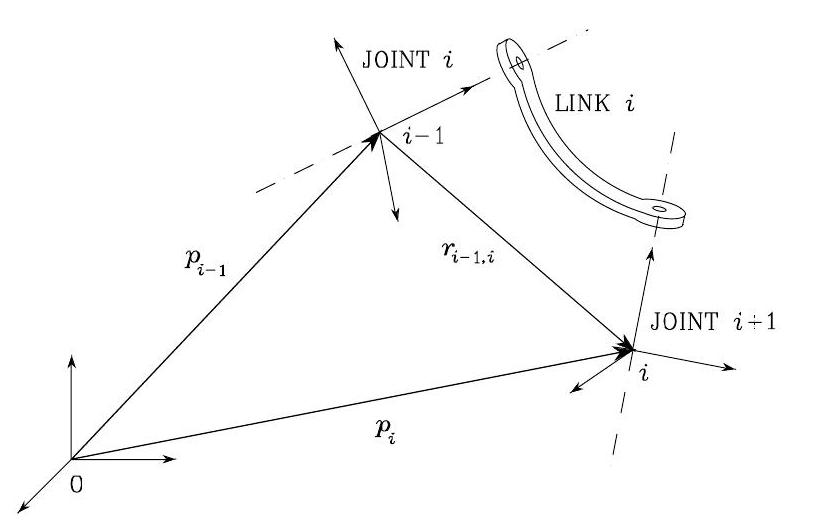
Fig. 54 Link \(i\) of a robot arm#
Linear (Translational) Velocity#
Let \(\boldsymbol{p}_{i-1}\) and \(\boldsymbol{p}_{i}\) be the position of the origins of Frame \(i-1\) and Frame \(i\), respectively. Also, let \(\boldsymbol{r}_{i-1, i}^{i-1}\) denote the position of the origin of Frame \(i\) from the origin of Frame \(i-1\), expressed in Frame \(i-1\).
Let’s consider \(\boldsymbol{p}_{i-1}\) be position of Frame \(i-1\) in the reference frame (therefore, i omit the superscript here), and \(\boldsymbol{R}_{i-1}\) be the rotation of Frame \(i-1\) in the reference frame (i omit the superscript again). Then, the position of Frame \(i\) in the reference frame is
Before we proceed, a question: how to obtain \(\boldsymbol{p}_{i-1}\) and \(\boldsymbol{R}_{i-1}\)? and how to obtain \(\boldsymbol{r}_{i-1, i}^{i-1}\)?
Similar to (10), taking the derivative of both sides in the above equation with respect to time \(t\), we have
Here, we define \(\boldsymbol{v}_{i-1, i}=\boldsymbol{R}_{i-1}\dot{\boldsymbol{r}}_{i-1, i}^{i-1}\), which is local translational velocity of Frame \(i\) in Frame \(i-1\), but expressed in the reference frame. Please carefully look at how first row becomes second row, and ask yourself what each term stands for on the second row, similar to how we have analyzed to(11).
Note
Now let’s think about what happens to (13) if joint \(i\) is revolute joint. In that case,
how to compute \(\boldsymbol{r}_{i-1, i}\)? Hint: think about forward kinematics.
what is \(\boldsymbol{v}_{i-1, i}\)? Hint: think about what is the relative motion of Frame \(i\) in Frame \(i-1\). You may answer:
But what is \(\boldsymbol{\omega}_{i-1, i}\)? Actually, it is relative angular velocity of Frame \(i\) in Frame \(i-1\), expressed in the reference frame.
So, next quesetion, hwo to compute \(\boldsymbol{\omega}_{i-1, i}\)? Actually
What is \(\boldsymbol{z}_{i-1}\)? This is question for you!
Combine (13), (14) and (15), we have: If Joint \(i\) is revolute
Note
Now let’s think about what happens to (13) if joint \(i\) is prismatic joint. In that case,
what is \(\boldsymbol{v}_{i-1, i}\)? Hint: think about what is the relative motion of Frame \(i\) in Frame \(i-1\). Actually
Combine (13), (14) and (16), we have: If Joint \(i\) is prismatic
Angular Velocity#
Next, let’s consider the rotation of Frame \(i\) in the reference frame (omit the superscipt 0 again)
Its time derivative is
where \(\boldsymbol{\omega}_{i-1, i}^{i-1}\) denotes the angular velocity of Frame \(i\) with respect to Frame \(i-1\) expressed in Frame \(i-1\). The second term on the right-hand side of (17) can be rewritten as
by recalling the property of the skew-symmetric matrix in (9). Then,
If we cancel out all \( \boldsymbol{R}_{i}\) on both sides of (18), we can get
Thus, the angular velocity \(\boldsymbol{\omega}_{i}\) of Link \(i\) depends only on the angular velocity \(\boldsymbol{\omega}_{i-1}\) of Link \(i-1\) and their relative angular velocity \(\boldsymbol{\omega}_{i-1, i}\).
Note
Now let’s think about what happens to (19) if joint \(i\) is revolute joint. In that case, what is \(\boldsymbol{\omega}_{i-1, i}\) and how to compute it?
Actually, it is (15)! Combine (19) and (15), we have: If Joint \(i\) is revolute
Note
Now let’s think about what happens to (19) if joint \(i\) is prismatic. In that case, what is \(\boldsymbol{\omega}_{i-1, i}\) and how to compute it?
Actually, it is \(0\)! Thus, we have: If Joint \(i\) is prismatic
Summary#
Considering different joint types for Joint \(i\) at a robot arm, according to (13) and (19), we can obtain
Important
If Joint \(i\) is prismatic
If Joint \(i\) is revolute
