Numerical Inverse Kinematics

Recall IK problems: given a desired end-effector pose \(\boldsymbol{x}_{d}\) (in operational space), we want to find the joint vector \(\boldsymbol{q}\) such that \(\boldsymbol{k}(\boldsymbol{q})=\boldsymbol{x}_d\). Here, \(\boldsymbol{k}(\cdot)\) is the forward kinematics. In this chapter, we will show how to use Jacobian to solve this problem numerically. Let’s consider

\[ \dot{\boldsymbol{x}}_{e}=\boldsymbol{J}_{A}(\boldsymbol{q}) \dot{\boldsymbol{q}} \]

with \(\boldsymbol{J}_{A}(\boldsymbol{q})\) is Jacobian (you will see why we use \(\boldsymbol{J}_{A}(\boldsymbol{q})\) instead of \(\boldsymbol{J}(\boldsymbol{q})\) to denote the Jacobian at the end of this lecture).

To solve the above IK, we define the following operational space error between the desired \(\boldsymbol{x}_{d}\) and the current end-effector pose \(\boldsymbol{x}_{e}\):

(23)\[\boldsymbol{e}=\boldsymbol{x}_{d}-\boldsymbol{x}_{e}=\boldsymbol{x}_{d}-\boldsymbol{k}(\boldsymbol{q}) \]

Consider the time derivative of (23)

(24)\[\dot{\boldsymbol{e}}=\dot{\boldsymbol{x}}_{d}-\dot{\boldsymbol{x}}_{e}=\dot{\boldsymbol{x}}_{d}-\boldsymbol{J}_{A}(\boldsymbol{q}) \dot{\boldsymbol{q}}\]

The above (24) is called error dynamics, as it show ODE of end-effector pose error \(\boldsymbol{e}(t)\) over time \(t\). Here, \(\dot{\boldsymbol{q}}\) can be viewed as the control input. From a control perspective, we want to find a feedback control law

\[\dot{\boldsymbol{q}}= \text{Controller}({\boldsymbol{x}}_d, \dot{\boldsymbol{x}}_d, {\boldsymbol{q}}, {\boldsymbol{e}})\]

such that, when plug the controller to the error dynamics, \(\boldsymbol{e}(t)\rightarrow 0\) as \(t\rightarrow \infty\). The different controllers leads to different IK algorithms.

Jacobian Inverse or Newton-Raphson Method

Important

In Jacobian Inverse IK method, we set \(\dot{\boldsymbol{q}}= \text{Controller}({\boldsymbol{x}}_d, \dot{\boldsymbol{x}}_d, {\boldsymbol{q}}, {\boldsymbol{e}})\) specifically as

\[\begin{split}\dot{\boldsymbol{q}}= \begin{cases} \boldsymbol{J}_{A}^{-1}(\boldsymbol{q})\left(\dot{\boldsymbol{x}}_{d}+\boldsymbol{K} \boldsymbol{e}\right) \quad\quad\text{for non-redundant robot arms} \\[10pt] \boldsymbol{J}_{A}^{\dagger}\left(\dot{\boldsymbol{x}}_{d}+\boldsymbol{K e}\right)+\left(\boldsymbol{I}_{n}-\boldsymbol{J}_{A}^{\dagger} \boldsymbol{J}_{A}\right) \dot{\boldsymbol{q}}_{\text{ref}} \quad\quad\text{for redundant robot arms} \end{cases}\end{split}\]

Here \(\boldsymbol{K}\) is a positive definite (usually diagonal) matrix, and \({\boldsymbol{q}}_{\text{ref}}\) is any reference joint velocity, which can be set based on a second objective in the previous chapter. \(\boldsymbol{J}_{A}^{\dagger}\) is the pseudo-inverse of Jacobian: \(\boldsymbol{J}_{A}^{\dagger}=\boldsymbol{J}_{A}^{T}\left(\boldsymbol{J}_{A} \boldsymbol{J}_{A}^{T}\right)^{-1}\).

Let’s next verify if the above controller can solve the IK or not, by examining if the error dynamics is converging to 0. Submitting the above controllers into the error dynamics, it easy to verify that

(25)\[\dot{\boldsymbol{e}}+\boldsymbol{K} \boldsymbol{e}=0 .\]

If \(\boldsymbol{K}\) is a positive definite (usually diagonal) matrix, (25) is asymptotically stable. The error tends to zero along the trajectory with a convergence rate that depends on the eigenvalues of \(\boldsymbol{K}\).

Background from Linear Control Systems course

Generally, given an ordinary differential equation (ODE)

\[\dot{\boldsymbol{e}}+\boldsymbol{K} \boldsymbol{e}=0\]

the solution \(\boldsymbol{e}(t)\) to the above ODE is

\[\boldsymbol{e}(t)=e^{\boldsymbol{-K}t}\boldsymbol{e}(0)\]

In particular, if \(\boldsymbol{K}\) is diagonal, say

\[\begin{split}\boldsymbol{K}=\begin{bmatrix} \lambda_1& & &\\ &\lambda_2 & & \\ & & \ddots &\\ & & & \lambda_r \end{bmatrix},\end{split}\]

the solution is

\[\begin{split}\boldsymbol{e}(t)=\begin{bmatrix} e^{-\lambda_1t}& & &\\ &e^{-\lambda_2t} & & \\ & & \ddots &\\ & & & e^{-\lambda_rt} \end{bmatrix}\boldsymbol{e}(0)\end{split}\]

Therefore, only if \(\lambda_1, \lambda_2, ...\lambda_r>0\), \(\boldsymbol{e}(t)\rightarrow \boldsymbol{0}\) as \(t\rightarrow \infty\).

The block scheme for the above IK algorithm is shown below (non-redundant robot arm), where \(\boldsymbol{k}(\cdot)\) means the direct kinematics function.

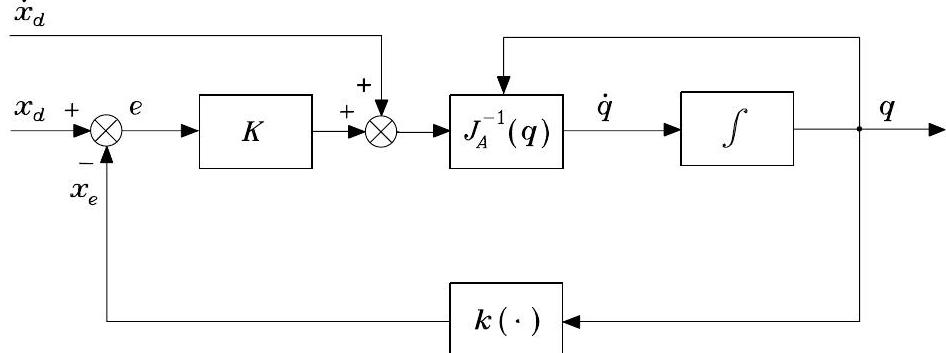
Fig. 64 IK algorithm with Jacobian inverse

Why it’s also named Newton-Raphson method?

The naming of Newton-Raphson method comes from the perspective of “IK as solving nonlinear equations”

Specifically, consider the following nonlinear equation from FK

(26)\[\boldsymbol{k}(\boldsymbol{q})=\boldsymbol{x}_d\]

given \(\boldsymbol{x}_d\).

Assume we have an initial guess \(\boldsymbol{q}_t\). One can approximate (26) at \(\boldsymbol{q}_k\) using the first-order Tyler expension:

\[\boldsymbol{k}(\boldsymbol{q})\approx\boldsymbol{k}(\boldsymbol{q}_t)+\boldsymbol{J}_{A}(\boldsymbol{q}_t)(\boldsymbol{q}-\boldsymbol{q}_t)=\boldsymbol{x}_d\]

By solving the above equation for \(\boldsymbol{q}\), one can obtain the next updated guess

\[\boldsymbol{q}_{t+1}=\boldsymbol{q}_t+\text{inv}\left(\boldsymbol{J}_{A}(\boldsymbol{q}_t)\right)(\boldsymbol{x}_d-\boldsymbol{t}(\boldsymbol{q}_t))=\boldsymbol{q}_t+\text{inv}\left(\boldsymbol{J}_{A}(\boldsymbol{q}_t)\right)\boldsymbol{e}_t\]

where \(\text{inv}\) is the general inverse operation (inverse for square matrix or pseudo-inverse for non-square matrix). Typically, one also needs a step size before \(\text{inv}\left(\boldsymbol{J}_{A}(\boldsymbol{q}_t)\right)\) to stabilize the Newton-Raphson algorithm. The above results can be considered as the discrete-time version of the Jacobian Inverse IK algorithm with \(\dot{\boldsymbol{x}}_d=\boldsymbol{0}\).

Jacobian Transpose or Gradient-Based Method

Important

In Jacobian Transpose IK method, we set \(\dot{\boldsymbol{q}}= \text{Controller}({\boldsymbol{x}}_d, \dot{\boldsymbol{x}}_d, {\boldsymbol{q}}, {\boldsymbol{e}})\) specifically as

\[\dot{\boldsymbol{q}}=\boldsymbol{J}_{A}^{T}(\boldsymbol{q}) \boldsymbol{K} \boldsymbol{e}\]

Here \(\boldsymbol{K}\) is a positive definite (usually diagonal) matrix,

Let’s next find out if the above controller can solve the IK or not, by using the Lyapunov Stability.

Background about Lyapunov Stability

Consider the following error dynamics (ODE)

\[\dot{\boldsymbol{x}}(t)=\boldsymbol{f}(\boldsymbol{x}),\quad \text{given}\quad \boldsymbol{x}(0)\]

If there exists a Lyapunov function \(V(\boldsymbol{x})\) such that

• \(V(\boldsymbol{x})>0 \quad \forall \boldsymbol{x} \neq \mathbf{0}\)

• \(V(\mathbf{0})=0 \quad \text{only for} \quad \boldsymbol{x}=\boldsymbol{0}\)

• \(\dot{V}=\frac{dV}{dt}=(\frac{d V}{d\boldsymbol{x}})^T\dot{\boldsymbol{x}}=(\frac{d V}{d\boldsymbol{x}})^T \boldsymbol{f}(\boldsymbol{x})<0 \quad \forall \boldsymbol{x}\)

then, \({\boldsymbol{x}}(t)\rightarrow \boldsymbol{0}\) as \(t\rightarrow \infty\) (the error is converging).

Consider \(\dot{\boldsymbol{x}}_{d}=\mathbf{0}\). Let’s use Lyapunov function to find controller such that the error dynamics (24) is stablizing. Let’s choose Lyapunov function

\[V(\boldsymbol{e})=\frac{1}{2} \boldsymbol{e}^{T} \boldsymbol{K} \boldsymbol{e}\]

where \(\boldsymbol{K}\) is a symmetric positive definite matrix. Obviously,

\[V(\boldsymbol{e})>0 \quad \forall \boldsymbol{e} \neq \mathbf{0}, \quad V(\mathbf{0})=0 \quad \text{only for} \quad \boldsymbol{e}=\boldsymbol{0}\]

Differentiating \(V(\boldsymbol{e})\) with respect to time gives

\[\dot{V}=\boldsymbol{e}^{T} \boldsymbol{K} \dot{\boldsymbol{x}}_{d}-\boldsymbol{e}^{T} \boldsymbol{K} \dot{\boldsymbol{x}}_{e}=\boldsymbol{e}^{T} \boldsymbol{K} \dot{\boldsymbol{x}}_{d}-\boldsymbol{e}^{T} \boldsymbol{K} \boldsymbol{J}_{A}(\boldsymbol{q}) \dot{\boldsymbol{q}}\]

At this point, since \(\boldsymbol{\dot{x}}_d=\boldsymbol{0}\), if we choose

\[\dot{\boldsymbol{q}}=\boldsymbol{J}_{A}^{T}(\boldsymbol{q}) \boldsymbol{K} \boldsymbol{e}\]

This leads to

\[\dot{V}=-\boldsymbol{e}^{T} \boldsymbol{K} \boldsymbol{J}_{A}(\boldsymbol{q}) \boldsymbol{J}_{A}^{T}(\boldsymbol{q}) \boldsymbol{K} \boldsymbol{e}\]

\(\dot{V}\) is negative definite, under the assumption of full rank for \(\boldsymbol{J}_{A}(\boldsymbol{q})\). \(\dot{V}<0\) with \(V>0\) implies the error dynamics will stabilize to \(\boldsymbol{e}=\mathbf{0}\), according to Lyapunov Stablity. The block scheme for the Jacobian transpose IK algorithm is shown below.

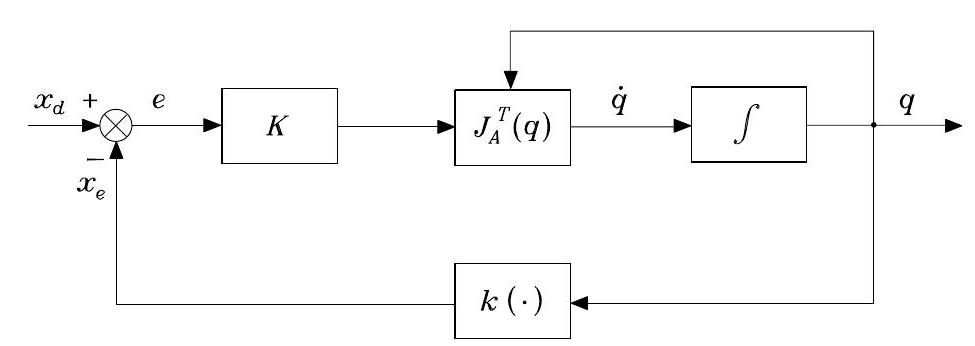
Fig. 65 Block scheme of the inverse kinematics algorithm with Jacobian transpose

Why it’s also named Gradient-Based Method?

Specifically, when \(\dot{\boldsymbol{x}}_d=\boldsymbol{0}\), consider we want to find the joint value \(\boldsymbol{q}\) by minimizing the error of

\[\min_{\boldsymbol{q}}\quad\frac{1}{2}||\boldsymbol{k}(\boldsymbol{q})-\boldsymbol{x}_d||^2\]

The gradient descent to update current guess \(\boldsymbol{q}_k\) to next \(\boldsymbol{q}_{k+1}\)

\[\boldsymbol{q}_{k+1}=\boldsymbol{q}_{k}-\alpha{\left(\frac{d\boldsymbol{k}(\boldsymbol{q})}{d\boldsymbol{q}}\bigg\rvert_{\boldsymbol{q}=\boldsymbol{q}_k}\right)}^{T}(\boldsymbol{k}(\boldsymbol{q})-\boldsymbol{x}_d)=\boldsymbol{q}_{k}+\alpha{\boldsymbol{J}_{A}(\boldsymbol{q}_k)}^{T}\boldsymbol{e}_k\]

where \(\alpha\) is the gradient step size. The above results can be considered as the discrete-time version of the Jacobian transpose IK algorithm if \(\boldsymbol{\dot{x}}_d=0\).

Definition of End-effector Error

Both IK algorithms above require computing the end-effector error. It is straightforward to define the position error of the end-effector

\[\boldsymbol{e}_{P}=\boldsymbol{p}_{d}-\boldsymbol{p}_{e}(\boldsymbol{q})\]

where \(\boldsymbol{p}_{d}\) and \(\boldsymbol{p}_{e}\) denote respectively the desired and computed end-effector positions. Its time derivative is

\[\dot{\boldsymbol{e}}_{P}=\dot{\boldsymbol{p}}_{d}-\dot{\boldsymbol{p}}_{e} .\]

However, the problem arises when we define the end-effector orientation error. In the following, let’s consider the typical Euler-Angles representations and its error definition.

Euler-Angles Error

The orientation error using Euler angles is

\[\boldsymbol{e}_{O}=\boldsymbol{\phi}_{d}-\boldsymbol{\phi}_{e}(\boldsymbol{q})\]

where \(\boldsymbol{\phi}_{d}\) and \(\boldsymbol{\phi}_{e}\) denote respectively the desired and computed Euler angles of the end-effector. Its time derivative is

\[\dot{\boldsymbol{e}}_{O}=\dot{\boldsymbol{\phi}}_{d}-\dot{\boldsymbol{\phi}}_{e}\]

In order to apply any of the above IK algorithms, we need to find a Jacobian in terms of

\[\begin{split}\dot{\boldsymbol{x}}_{e}=\left[\begin{array}{c} \dot{\boldsymbol{p}}_{e} \\ \dot{\boldsymbol{\phi}}_{e} \end{array}\right] = \boldsymbol{J}_{A} \dot{\boldsymbol{q}} = \begin{bmatrix} \boldsymbol{J}_{P}(\boldsymbol{q})\\ \boldsymbol{J}_{\phi}(\boldsymbol{q}) \end{bmatrix} \dot{\boldsymbol{q}} \end{split}\]

As you can see, compared to the Jacobian \( \boldsymbol{J}=\begin{bmatrix} \boldsymbol{J}_{P}(\boldsymbol{q})\\ \boldsymbol{J}_{O}(\boldsymbol{q}) \end{bmatrix}\) we have learned in the Jacobian lecture, the linear Jacobian \(\boldsymbol{J}_{P}(\boldsymbol{q})\) remains the same as before, the only difference is the angular Jacobian \(\boldsymbol{J}_{O}(\boldsymbol{q})\) becomes

\[ \dot{\boldsymbol{\phi}}_{e}= \boldsymbol{J}_{\phi}(\boldsymbol{q}) \dot{\boldsymbol{q}} \]

We call the new Jacobian matrix

\[\begin{split} \boldsymbol{J}_{A}(\boldsymbol{q})=\begin{bmatrix} \boldsymbol{J}_{P}(\boldsymbol{q})\\ \boldsymbol{J}_{\phi}(\boldsymbol{q}) \end{bmatrix} \end{split}\]

the analytical Jacobian(recall \(\boldsymbol{J}\) is called geometrical Jacobian or Jacobian). This is the reason why we in the above used \(\boldsymbol{J}_{A}\) instead of \(\boldsymbol{J}\)!

Next question, how do we find \(\boldsymbol{J}_{A}(\boldsymbol{q})\) from \(\boldsymbol{J}\)? To do so, we may need find a mapping

\[\begin{split}\left[\begin{array}{c} \dot{\boldsymbol{p}}_{e} \\ \boldsymbol{\omega}_{e} \end{array}\right] = \underbrace{\begin{bmatrix} \boldsymbol{I} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{N}\left(\phi_{e}\right) \end{bmatrix}}_{\boldsymbol{T}} \left[\begin{array}{c} \dot{\boldsymbol{p}}_{e} \\ \dot{\boldsymbol{\phi}}_{e} \end{array}\right]\end{split}\]

such that

\[\boldsymbol{J}_{A}(\boldsymbol{q}) = \boldsymbol{T}^{-1} \boldsymbol{J}(\boldsymbol{q})\]

In the following, we will find out the mapping

\[\boldsymbol{\omega}_{e}=\boldsymbol{N}\left(\phi_{e}\right)\dot{\boldsymbol{\phi}}_{e}\]

for the Euler ZYZ Angle \({\boldsymbol{\phi}}_{e}=[{\varphi}, {\vartheta}, \psi]^T\).

Recall the rotation induced from the Euler ZYZ Angle. The angualr velocities \(\dot{\varphi}, \dot{\vartheta}, \dot\psi\) is always with respect to the current frame, as shown in Fig. 66.

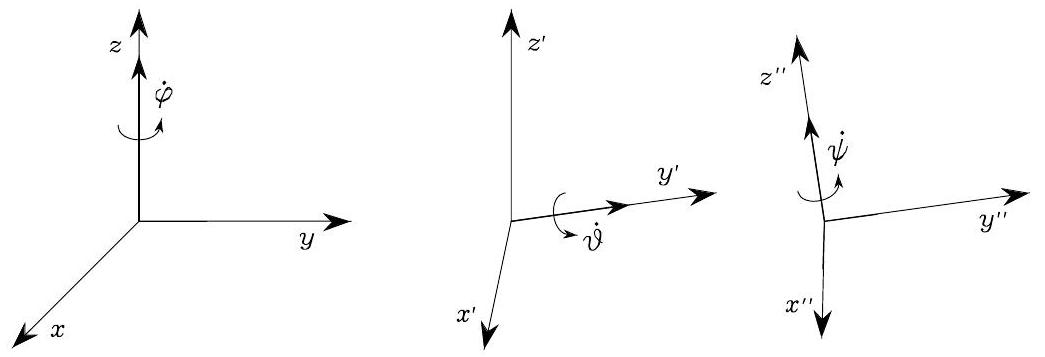
Fig. 66 Rotational velocities of Euler angles ZYZ in current frame

Therefore, to compute \(\boldsymbol{\omega}_{e}\), we just need to first, express each Euler angle velocity \(\dot{\varphi}, \dot{\vartheta}, \dot\psi\) from its respective current from to the reference frame, and second, sum them up!

• The angular velocity corresponding to \(\dot{\varphi}\) is

\[\dot{\varphi}\left[\begin{array}{lll}0 & 0 & 1\end{array}\right]^{T}\]

• The angular velocity corresponding to \(\dot{\vartheta}\) is

\[\dot{\vartheta}\left[\begin{array}{lll}-s_{\varphi} & c_{\varphi} & 0\end{array}\right]^{T}\]

• The angular velocity corresponding to \(\dot{\psi}\) is

\[\dot{\psi}\left[\begin{array}{lll}c_{\varphi} s_{\vartheta} & s_{\varphi} s_{\vartheta} & c_{\vartheta}\end{array}\right]^{T}\]

Thus,

\[\begin{split}\boldsymbol{N}\left(\phi_{e}\right) =\left[\begin{array}{ccc} 0 & -s_{\varphi} & c_{\varphi} s_{\vartheta} \\ 0 & c_{\varphi} & s_{\varphi} s_{\vartheta} \\ 1 & 0 & c_{\vartheta} \end{array}\right] .\end{split}\]