Operational Space Control

The goal of operational space control (OSC) is to control the robot to track the desired end-effector pose \(\boldsymbol{x}_d\) and velocity \(\boldsymbol{\dot{x}}_d\) given in the operational space. Consider a a \(n\)-joint robot arm without external end-effector forces and any joint friction. The equation of motion of the robot arm is

(64)\[ \boldsymbol{B}(\boldsymbol{q}) \ddot{\boldsymbol{q}}+\boldsymbol{C}(\boldsymbol{q}, \dot{\boldsymbol{q}}) \dot{\boldsymbol{q}}+\boldsymbol{g}(\boldsymbol{q})=\boldsymbol{u}\]

The controller we want to design is in the general form of

(65)\[ \boldsymbol{u}=\textbf{controller}(\boldsymbol{q}, \boldsymbol{\dot{q}}, \boldsymbol{x}_d, \boldsymbol{\dot{x}}_d)\]

i.e., the controller takes as input the robot arm’s current joint position \(\boldsymbol{q}\), current joint velocity \(\boldsymbol{\dot{q}}\), the desired end-effector pose \(\boldsymbol{x}_d\), and desired end-effector velocity \(\boldsymbol{\dot{x}}_d\), and outputs the joint torque \(\boldsymbol{u}\).

The closed-loop dynamics with controller is

(66)\[ \boldsymbol{B}(\boldsymbol{q}) \ddot{\boldsymbol{q}}+\boldsymbol{C}(\boldsymbol{q}, \dot{\boldsymbol{q}}) \dot{\boldsymbol{q}}+\boldsymbol{g}(\boldsymbol{q})=\textbf{controller}(\boldsymbol{q}, \boldsymbol{\dot{q}}, \boldsymbol{x}_d, \boldsymbol{\dot{x}}_d)\]

We define the end-effector pose error:

(67)\[ \boldsymbol{e}=\boldsymbol{x}_{d}-\boldsymbol{x} \]

and end-effector velocity error:

(68)\[ \boldsymbol{\dot e}=\boldsymbol{\dot x}_{d}-\boldsymbol{\dot x}=\boldsymbol{\dot x}_{d}-\boldsymbol J (\boldsymbol{q})\boldsymbol{\dot q} \]

with with \(\boldsymbol{x}\) the current/actual robot end-effector pose, and \(\boldsymbol{x}\) the current/actual robot end-effector pose.

Controller 1: PD Control with Gravity Compensation

Given a stationary end-effector pose \(\boldsymbol{x}_{d}\) (\(\boldsymbol{\dot x}_{ d}=\boldsymbol{0}\)), we want to design a controller (65) such that from any initial robot configuration \(\boldsymbol{q}_0\), the controlled robot arm (66) will eventually reach \(\boldsymbol{x}_{d}\). That means

\[\boldsymbol{e}(t)\rightarrow \boldsymbol{0}\quad \text{as}\quad t\rightarrow \infty\]

PD Control with Gravity Compensation

The controller for PD control with gravity compensation follows

(69)\[ \boldsymbol{u}=\underbrace{\boldsymbol{g}(\boldsymbol{q})}_{\text{gravitational compensation}}+ \underbrace{\boldsymbol{J}^{T}(\boldsymbol{q}) \boldsymbol{K}_{P} {(\boldsymbol{x}_d-\boldsymbol{x})}}_{\text{proportional control}}\quad\underbrace{-\boldsymbol{J}^{T}(\boldsymbol{q})\boldsymbol{K}_{D} \boldsymbol{J}(\boldsymbol{q})\dot{\boldsymbol{q}}}_{\text{derivative control}}\]

with \(\boldsymbol{K}_{P}\) and \(\boldsymbol{K}_{D}\) are positive definite matrices.

Lyapunov stability proof for PD controller (click to expand)

Below, we will prove (69) is stablizing the robot to the desired end-effector position, based on the Lyapunov method (see background of Lyapunov method in Numerical Inverse Kinematics).

First, we take the vector \(\begin{bmatrix}\boldsymbol{e}\\ \boldsymbol{\dot{q}}\end{bmatrix}\) as the system state. Choose the following positive definite quadratic form as Lyapunov function:

(70)\[\begin{split}V(\dot{\boldsymbol{q}}, {\boldsymbol{e}})=\frac{1}{2} \dot{\boldsymbol{q}}^{T} \boldsymbol{B}(\boldsymbol{q}) \dot{\boldsymbol{q}}+\frac{1}{2} {\boldsymbol{e}}^{T} \boldsymbol{K}_{P} {\boldsymbol{e}}>0 \quad \forall \begin{bmatrix}\boldsymbol{e}\\ \boldsymbol{\dot{q}}\end{bmatrix} \neq \mathbf{0}\end{split}\]

with \(\boldsymbol{K}_{P}\) a positive definite matrix.

Then,

\[\dot{V}=\dot{\boldsymbol{q}}^{T} \boldsymbol{B}(\boldsymbol{q}) \ddot{\boldsymbol{q}}+\frac{1}{2} \dot{\boldsymbol{q}}^{T} \dot{\boldsymbol{B}}(\boldsymbol{q}) \dot{\boldsymbol{q}}+\dot{\boldsymbol{e}}^{T} \boldsymbol{K}_{P} {\boldsymbol{e}}\]

Since \(\dot{\boldsymbol{x}}_{d}=\mathbf{0}\),

\[\dot{{\boldsymbol{e}}}=-\dot{\boldsymbol{x}}=-\boldsymbol{J}(\boldsymbol{q}) \dot{\boldsymbol{q}}\]

and then

(71)\[\dot{V}=\dot{\boldsymbol{q}}^{T} \boldsymbol{B}(\boldsymbol{q}) \ddot{\boldsymbol{q}}+\frac{1}{2} \dot{\boldsymbol{q}}^{T} \dot{\boldsymbol{B}}(\boldsymbol{q}) \dot{\boldsymbol{q}}-\dot{\boldsymbol{q}}^{T} \boldsymbol{J}^{T}(\boldsymbol{q}) \boldsymbol{K}_{P} {\boldsymbol{e}}\]

Similar to the derivation in joint space PD controller, we replace \(\boldsymbol{B}\ddot{\boldsymbol{q}}\) in (71) form closed-loop dynamics

(72)\[\boldsymbol{B}(\boldsymbol{q}) \ddot{\boldsymbol{q}}+\boldsymbol{C}(\boldsymbol{q}, \dot{\boldsymbol{q}}) \dot{\boldsymbol{q}}+\boldsymbol{F} \dot{\boldsymbol{q}}+\boldsymbol{g}(\boldsymbol{q})=\boldsymbol{g}(\boldsymbol{q})+\boldsymbol{J}^{T}(\boldsymbol{q}) \boldsymbol{K}_{P} {\boldsymbol{e}}-\boldsymbol{J}^{T}(\boldsymbol{q}) \boldsymbol{K}_{D} \boldsymbol{J}(\boldsymbol{q}) \dot{\boldsymbol{q}}\]

and consider the property \(\dot{\boldsymbol{B}}-2 \boldsymbol{C}\) is a skew-symmetric matrix. Then, (71) becomes

(73)\[\dot{V}=-\dot{\boldsymbol{q}}^{T} \boldsymbol{J}^{T}(\boldsymbol{q}) \boldsymbol{K}_{D} \boldsymbol{J}(\boldsymbol{q}) \dot{\boldsymbol{q}} \quad <0, \quad \forall \boldsymbol{\dot{q}}\quad\text{with} \quad \boldsymbol{J}(\boldsymbol{q})\dot{\boldsymbol{q}} \neq \mathbf{0}\]

which says the Lyapunov function decreases as long as \(\boldsymbol{J}(\boldsymbol{q})\dot{\boldsymbol{q}} \neq \mathbf{0}\). Thus, the system reaches an equilibrium pose, with condition \(\dot{V}= 0\) and \(\boldsymbol{J}(\boldsymbol{q})\dot{\boldsymbol{q}}=\mathbf{0}\).

We consider the non-redundant non-singularity of matrix \(\boldsymbol{J}(\boldsymbol{q})\). Then, the equilibrium condition \(\boldsymbol{J}(\boldsymbol{q})\dot{\boldsymbol{q}}=\mathbf{0}\) means that \(\dot{\boldsymbol{q}}=\mathbf{0}\) and further \(\ddot{\boldsymbol{q}} =\mathbf{0}\). To find the robot equilibrium configuration, we look at (72). With the condition \(\dot{\boldsymbol{q}}=\mathbf{0}\), it follows that \(\ddot{\boldsymbol{q}} =\mathbf{0}\), and then the above becomes

(74)\[\boldsymbol{J}^{T}(\boldsymbol{q}) \boldsymbol{K}_{P} {\boldsymbol{e}}=\mathbf{0}\quad \rightarrow\quad {\boldsymbol{e}}=\boldsymbol{x}_{d}-\boldsymbol{x}_{e}=\mathbf{0}\]

This concludes that the controlled robot arm will asymptotically reach \(\boldsymbol{x}_d\).

The corresponding control diagram is shown below.

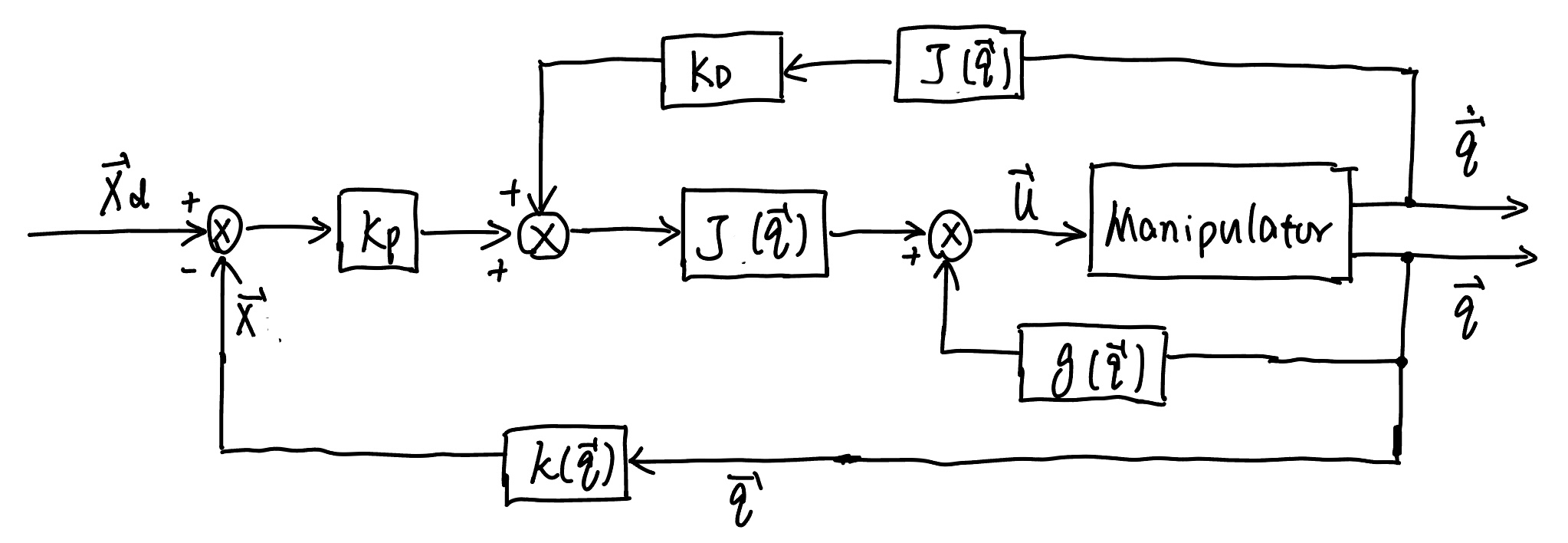
Fig. 69 Block diagram of operational space PD control with gravity compensation

Controller 2: Inverse Dynamics Control

One limitation of the OSC PD Control is that the controller can only follow a stationary desired \(\boldsymbol{x}_d\) , but is not good at tracking a fast-changing desired \(\boldsymbol{x}_d\) (i.e., \(\boldsymbol{\dot x}_d\neq \boldsymbol{0}\)). Inverse Dynamics Control can be used.

Inverse dynamics control

(75)\[ \boldsymbol{u}=\boldsymbol{B}(\boldsymbol{q}) \boldsymbol{y}+\boldsymbol{C}(\boldsymbol{q}, \dot{\boldsymbol{q}}) \dot{\boldsymbol{q}}+\boldsymbol{g}(\boldsymbol{q})\]

with

(76)\[ \boldsymbol{y}=\boldsymbol{J}^{-1}(\boldsymbol{q})\left(\ddot{\boldsymbol{x}}_{d}+\boldsymbol{K}_{D} \dot{{\boldsymbol{e}}}+\boldsymbol{K}_{P} {\boldsymbol{e}}-\dot{\boldsymbol{J}}(\boldsymbol{q}, \dot{\boldsymbol{q}}) \dot{\boldsymbol{q}}\right)\]

Here,

\[ \boldsymbol{K}_{P}=\operatorname{diag}\left\{\omega_{1}^{2}, \ldots, \omega_{r}^{2}\right\} \quad \boldsymbol{K}_{D}=\operatorname{diag}\left\{2 \zeta_{1} \omega_{1}, \ldots, 2 \zeta_{r} \omega_{r}\right\}\]

with with \(\zeta_i\) the damping ratio and \(\omega_{i}\) the natural frequency.

Stability proof for Inverse Dynamics Control (click to expand)

Plugging (75) to (76) to the closed-loop dynamics (66), we have the following error dynamics

\[\ddot{{\boldsymbol{e}}}+\boldsymbol{K}_{D} \dot{{\boldsymbol{e}}}+\boldsymbol{K}_{P} {\boldsymbol{e}}=\mathbf{0}\]

which describes the operational space error dynamics, with \(\boldsymbol{K}_{P}\) and \(\boldsymbol{K}_{D}\) determining the error convergence rate to zero. Typicaly we choose

\[ \boldsymbol{K}_{P}=\operatorname{diag}\left\{\omega_{1}^{2}, \ldots, \omega_{r}^{2}\right\} \quad \boldsymbol{K}_{D}=\operatorname{diag}\left\{2 \zeta_{1} \omega_{1}, \ldots, 2 \zeta_{r} \omega_{r}\right\}\]

with with \(\zeta_i\) the damping ratio and \(\omega_{i}\) the natural frequency. Then, the end-effector of the controlled robot arm will behave like a linear second-order (mass-spring-damper) system.

The resulting OCS inverse dynamics control diagram is shown below.

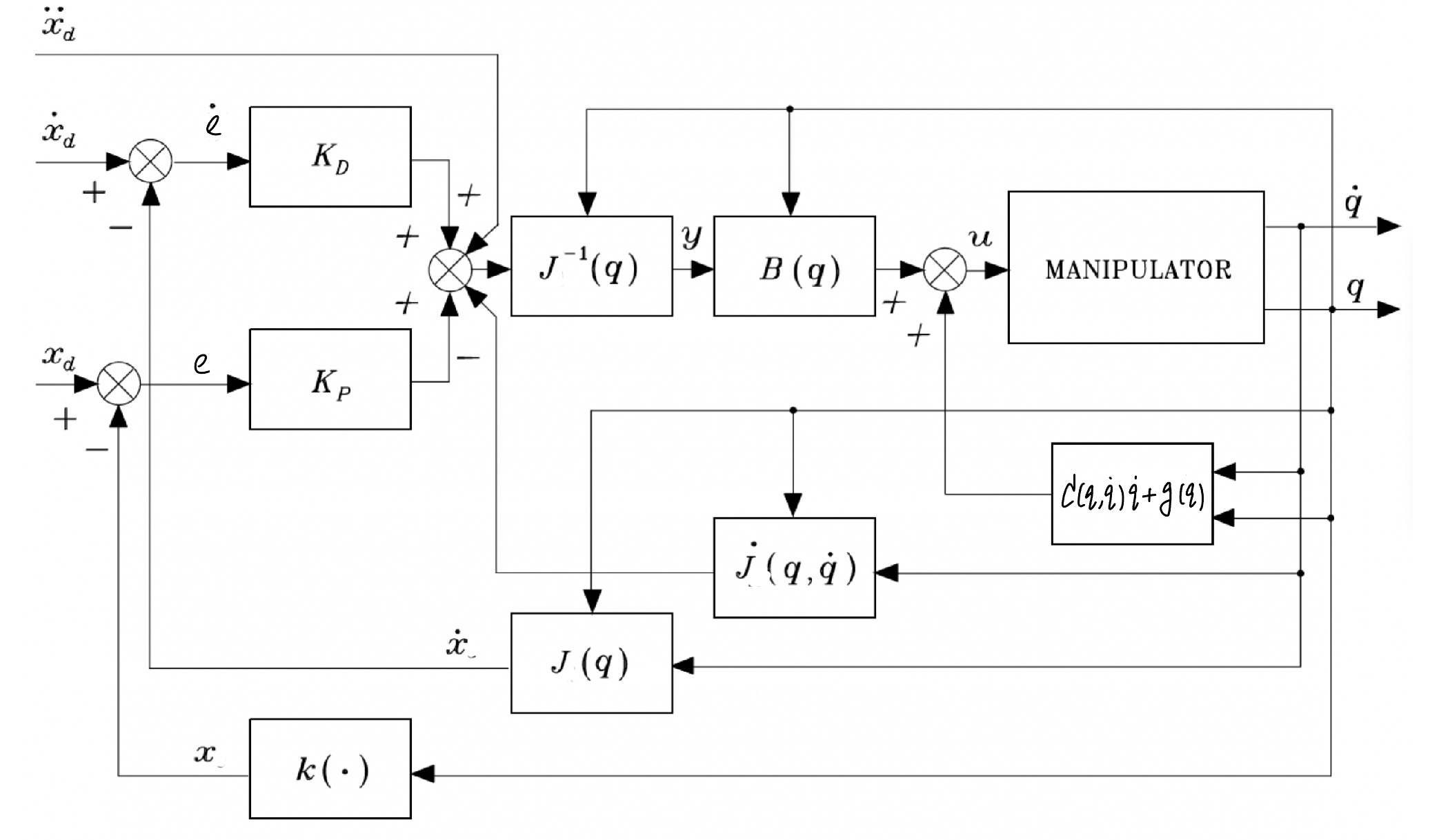
Fig. 70 Block scheme of operational space PD control with gravity compensation